chapter 5
We have mapped out the complete phase diagram of hard spherocylinders
as a function of the length-to-width ratio 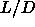 . Special
computational techniques were required to locate phase transitions in
the limit
. Special
computational techniques were required to locate phase transitions in
the limit 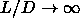 and in the close-packing limit for
and in the close-packing limit for
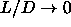 . The phase boundaries of five different phases
were established: the isotropic fluid, the liquid crystalline
smectic A and nematic phases, the orientationally-ordered solids ---
in AAA and ABC stacking --- and the plastic or rotator solid. The
rotator phase is unstable for
. The phase boundaries of five different phases
were established: the isotropic fluid, the liquid crystalline
smectic A and nematic phases, the orientationally-ordered solids ---
in AAA and ABC stacking --- and the plastic or rotator solid. The
rotator phase is unstable for 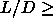 0.35 and the AAA crystal
becomes unstable for lengths smaller than
0.35 and the AAA crystal
becomes unstable for lengths smaller than 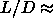 7. The triple
points isotropic-smectic-A-solid and isotropic-nematic-smectic-A are
estimated to occur at
7. The triple
points isotropic-smectic-A-solid and isotropic-nematic-smectic-A are
estimated to occur at 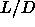 =3.1 and
=3.1 and  =3.5 respectively. For the
low
=3.5 respectively. For the
low 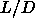 region, a modified version of the Gibbs-Duhem integration
method was used to calculate the isotropic-solid coexistence
curves. This method was also applied to the isotropic-nematic transition for
region, a modified version of the Gibbs-Duhem integration
method was used to calculate the isotropic-solid coexistence
curves. This method was also applied to the isotropic-nematic transition for 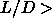 10. For large
10. For large 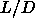 the simulation results approach the predictions
of the Onsager theory. In the limit
the simulation results approach the predictions
of the Onsager theory. In the limit 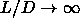 simulations were performed by application of a scaling technique. The
nematic-smectic-A transition for
simulations were performed by application of a scaling technique. The
nematic-smectic-A transition for 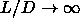 appears to
be continuous. As the nematic-smectic-A transition is certainly of
first order nature for
appears to
be continuous. As the nematic-smectic-A transition is certainly of
first order nature for 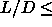 5, the tri-critical point is
presumably located between
5, the tri-critical point is
presumably located between 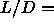
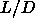 region, the plastic solid to aligned solid transition is first
order. Using a mapping of the dense sphero-cylinder system on a
lattice model, the initial slope of the coexistence curve could even
be computed in the close packing limit.
region, the plastic solid to aligned solid transition is first
order. Using a mapping of the dense sphero-cylinder system on a
lattice model, the initial slope of the coexistence curve could even
be computed in the close packing limit.
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
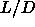 . Special
computational techniques were required to locate phase transitions in
the limit
. Special
computational techniques were required to locate phase transitions in
the limit 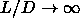 and in the close-packing limit for
and in the close-packing limit for
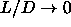 . The phase boundaries of five different phases
were established: the isotropic fluid, the liquid crystalline
smectic A and nematic phases, the orientationally-ordered solids ---
in AAA and ABC stacking --- and the plastic or rotator solid. The
rotator phase is unstable for
. The phase boundaries of five different phases
were established: the isotropic fluid, the liquid crystalline
smectic A and nematic phases, the orientationally-ordered solids ---
in AAA and ABC stacking --- and the plastic or rotator solid. The
rotator phase is unstable for 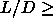 0.35 and the AAA crystal
becomes unstable for lengths smaller than
0.35 and the AAA crystal
becomes unstable for lengths smaller than 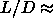 7. The triple
points isotropic-smectic-A-solid and isotropic-nematic-smectic-A are
estimated to occur at
7. The triple
points isotropic-smectic-A-solid and isotropic-nematic-smectic-A are
estimated to occur at 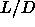 =3.1 and
=3.1 and  =3.5 respectively. For the
low
=3.5 respectively. For the
low 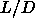 region, a modified version of the Gibbs-Duhem integration
method was used to calculate the isotropic-solid coexistence
curves. This method was also applied to the isotropic-nematic transition for
region, a modified version of the Gibbs-Duhem integration
method was used to calculate the isotropic-solid coexistence
curves. This method was also applied to the isotropic-nematic transition for 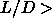 10. For large
10. For large 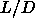 the simulation results approach the predictions
of the Onsager theory. In the limit
the simulation results approach the predictions
of the Onsager theory. In the limit 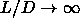 simulations were performed by application of a scaling technique. The
nematic-smectic-A transition for
simulations were performed by application of a scaling technique. The
nematic-smectic-A transition for 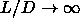 appears to
be continuous. As the nematic-smectic-A transition is certainly of
first order nature for
appears to
be continuous. As the nematic-smectic-A transition is certainly of
first order nature for 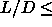 5, the tri-critical point is
presumably located between
5, the tri-critical point is
presumably located between 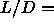
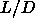 region, the plastic solid to aligned solid transition is first
order. Using a mapping of the dense sphero-cylinder system on a
lattice model, the initial slope of the coexistence curve could even
be computed in the close packing limit.
region, the plastic solid to aligned solid transition is first
order. Using a mapping of the dense sphero-cylinder system on a
lattice model, the initial slope of the coexistence curve could even
be computed in the close packing limit.