SMECTIC PHASE

  The smectic phase does not have an obvious reference state for which the free energy is known. Veerman [26] used the parallel spherocylinder system as a reference. However, the free energy of a parallel smectic itself is subject to numerical error. We chose to couple the spherocylinders with an harmonic spring to the smectic layer to which they belong and subsequently align them. In this way, the smectic phase can be transformed into what is essentially a 2D hard disk fluid for which the free energy is well known [56]. In principle, one could apply the Einstein integration method used in the previous section with one difference: the position field couples only the z-coordinates of the particles to the layer positions and leaves the x,y coordinates completely free. If we consider the first part of the integration, where the particle are confined to their layers, the free energy of smectic phase can be related to this planar system by

In the second integration, the difficulty arises that a infinite amount of aligning energy is needed to get all spherocylinders completely parallel.

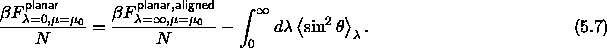
To keep the energy values finite, we subtract on both sides of this equation the free energy of an ideal rotator in the same field.

The excess free energy of the completely aligned planar system 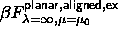is equal to the excess free energy of a 2D hard disk fluid. The free energy of the ideal planar system (with fixed center-of-mass) in the limit of large coupling constants is given by

The integral over the difference of the 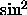terms in eqn. 5.9 is finite. We can change the integration boundaries by substituting .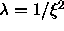

In conventional MC sampling, the statistical error of both terms in the integrand is larger than the difference itself. We therefore applied the following scheme to evaluate the difference directly in the Monte Carlo program. Instead of rotating a spherocylinder i around an angle 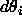we choose a completely new trial value of 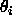from the probability distribution

This is the equilibrium distribution for an ideal rotator with a Hamiltonian according to eqn. 5.3 and results in the correct value for 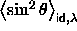. If no overlap occurs the trial move will be accepted and we will have

If an overlap does occur the trial move will be rejected and the particle will retain its old value. The difference now will be

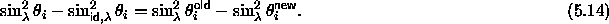
The statistical error in the average of the difference is always smaller than the average itself. This will enable us to determine the integrand more accurately. By combining eqns 5.6,5.9 and 5.11 the complete expression for free energy of the smectic phase follows

The excess hard disk free energy can be obtained by subtracting the ideal term 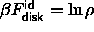from the free energy in ref. [56]. All integrations were carried out using Gauss-Legendre quadrature. To ensure that the 2D densities in the smectic layers are equal throughout the system we used shifted periodic boundaries. In our system the periodic boundaries in the x-direction are shifted exactly one layer period along the z-axis, while leaving them the same in the y and z direction. In this way, a particle leaving the simulation box at the left side will reenter the box at the right one layer higher. This particle can diffuse through the whole system, as there is effectively only one layer. This ensures that fluctuations in the number of particles per smectic layer can relax, even at high density where normal inter-layer diffusion is effectively frozen out.