NEMATIC-SMECTIC FREE ENERGY DIFFERENCE

  It turned out to be rather difficult to determine the first order nematic smectic coexistence region for 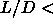5, because the location of the coexistence point appeared to be quite sensitive to errors in the free energy of the nematic and smectic phases. Therefore we calculated the free energy difference between a stable nematic and a stable smectic directly. In order to find a reversible path from the nematic to smectic we applied the following Hamiltonian

where n is the number of smectic layers, 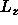the box length in the z-direction, 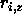the z-coordinate of particle i and 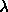the coupling parameter determining the strength of the smectic ordering. At low density this Hamiltonian will produce, by increasing 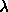, a gradual transition from a nematic to a smectic phase. We started with a smectic phase and applied a cosine field at large enough 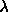. Subsequently, the smectic was expanded to lower density, while measuring the pressure. Finally, the cosine field was slowly turned off. The free energy difference now simply is

Of course, the value of 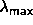should be chosen large enough that the first-order S-N transition is completely suppressed.