Next: Results Up: The Onsager limit Previous: The Onsager limit
Next: Results
Up: The Onsager limit
Previous: The Onsager limit
As we saw in the previous section, spherocylinders with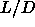 
=40 are
too small to compare properly with the bifurcation
results of Poniewierski for for 
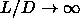and so it would be interesting to simulate a system
of spherocylinders in this limit.
At first sight this seems impossible because in general the system size scales
with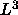 
. However, at finite reduced density 
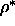, i.e. not in the
isotropic phase or low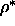 
nematic phase, the average angle 
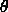that a particle makes with the director scales
as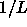 
, which means that the particles are (almost) completely aligned.
In this regime, we can bring the volume down to finite sizes by
scaling the system along the director (chosen to be along the z-axis) with a factor L. This will
change the shape of the particle from a spherocylinder to a shifted
cylinder of height 1 and diameter D (see figure 5.14).
The height of the cylinder is always 1 because the angle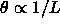 
and the difference in height 
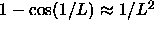vanishes as 
.
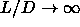The shift of the cylinder in the xy plane perpendicular to the
director is finite because it is given by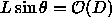 
in
the limit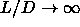 
.
The top and bottom end of the
cylinder are flat and always perpendicular to the director. The
hemispheres of the spherocylinder have completely disappeared by the
scaling procedure.
Because the shape of the particle is different from a spherocylinder we need a new overlap criterion. This is given by the shortest distance between two particle axes in the xy plane. In the xy plane a cut through the cylinder results in a circle of diameter D. Therefore, if the shortest distance is smaller than the diameter D, an overlap will occur.
Scaling of the box in this particular way will not effect the reduced
density because the close packing density will scale in the same
way as the number density.
The pressure will be multiplied by a factor L, whereas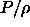 
remains
uneffected by the scaling.
We can therefore measure the equation of state of the Onsager limit system in the normal NPT ensemble.
Because the particles are free to shift any arbitrary amount in the xy plane it is convenient to keep the nematic director always along the z-axis. This can be achieved by starting with a complete aligned system and shift two particles with the same amount in opposite direction at every MC trial move. In order to avoid multiple overlaps, shifts larger than half the box-length are forbidden. Standard MC trial moves were not very effective in reproducing the collective motion of tilted layers. In the smectic phase, we therefore allowed for two neighboring layers to tilt collectively by equal but opposite amounts, so that the constraint of a constant director is satisfied.
. The solid lines are expansion branches, the
dotted lines are compression curves. The hysteresis around 
=0.5 is suggestive
of a first-order nematic to smectic phase transition.