Next: Results Up: Phase diagram in Previous: Phase diagram in
Next: Results
Up: Phase diagram in
Previous: Phase diagram in
The numerical study of the spherocylinder phase diagram for systems of
longer rods is not different in principle from the study for shorter
rods. However, in practice, there are many differences. Almost all
these differences imply that simulations of longer rods are more time
consuming. For one thing, the simulation of
long rods requires large system sizes. The simulation box should be
large enough
to accommodate at least two rod lengths in order to avoid
the situation that one particle can, at the same time, overlap with
more than one periodic image of another particle.
The number of particles required at a given
density scales with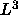 
whereas the number density at the I-N transition
is expected to scale as 
.
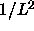In practice, it turns out that if we wish to impose the condition that
the box diameter is larger than 2L, then for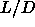 
=50 at the
isotropic-nematic transition, one needs at least 3000
particles. The disadvantage of using such a large number of particles
is that the simulations become very slow and, as a consequence, the
statistical accuracy tends to be poor.
We therefore decided to work with somewhat smaller systems where
multiple overlaps, although rare, are not completely excluded. Of
course, this implies that we must now also test for overlap with more
than one periodic image.
The possibility of two simultaneous overlaps with the same
particle is taken into account by doing three independent overlap
tests. Usually, the pair overlap test routine selects a first particle,
looks for the nearest periodic image of the second particle with
respect to the first one and calculates shortest distance between the
pair. There is an overlap if this distance is smaller than D. If
the box is smaller than 2 L more than one overlap is
possible, but not more than two. Figure 5.9 illustrates
this. In principle, particle A could overlap with B and its periodic images 
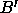and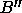 
,
but it cannot overlap with any of the other periodic images at the
same time provided the box length is larger than L+2D. For instance, A cannot overlap with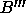 
if the
cylinder axis of A does not enter the periodic image of the box
containing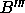 
.
We devised an overlap routine which looks for the three images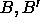 
and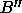 
and check
those for overlap in the usual way. This routine is applicable to both MD and
MC, including Gibbs-ensemble MC.
Although this routine seems more time-consuming because it has to
check for three overlaps instead of one, it is still preferable to
perform an overlap test for several periodic images than to perform
all simulations for a larger system.
In the region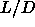 
=15 to 50 the isotropic-nematic transition was
studied both by Gibbs ensemble simulation [31,32,33] and
Gibbs-Duhem integration [84].
| Table: |
Pressure and densities of coexisting isotropic and nematic
phases for hard spherocylinders with aspect ratios 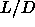 between 15
and 50. The coexistence data in this table were obtained using the
modified Gibbs-Duhem integration procedure described in the text.
Units as in table 5.3. |
We started with an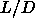 
=40 isotropic random configuration at low
density and a perfectly aligned configuration at high density. Using
Gibbs ensemble MC these configurations were equilibrated to
coexistence. This coexistence was used to perform a quick standard
Gibbs-Duhem integration in the range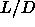 
=15--50 to obtain an initial
estimate for the coexistence curve. Subsequently,
we used this set of configurations to start the ``parallel''
Gibbs-Duhem technique described in section 5.3.3.
This calculation was continued until the coexistence curve had fully
converged.
As a check, Gibbs ensemble MC simulation were
also performed for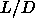 
= 20, 30, 50 and 60.
| Table: |
Pressure and densities of coexisting isotropic and nematic
phases for hard spherocylinders with aspect ratios 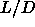 between 15
and 50. The coexistence data in this table were obtained using
Gibbs-ensemble simulations.
Units as in table 5.3. |
between 15 and 60. The
drawn curves have been obtained by modified Gibbs-Duhem integration.
The open circles denote the results of Gibbs-ensemble simulations (see
text)
-limit. In order to facilitate comparison with the Onsager limit,
all densities are expressed in units 
. On the x-axis, we plot 
rather than 
. Hence, the
Onsager limit corresponds to the value 
=0. Note that our
simulation results approach smoothly towards the exact solution of the
Onsager model, except for a few points at low 
. 