SOLID PHASE

  The strong first order transition separating the solid phase from the other phases rules out the integration along the equation of state. Instead, we choose as reference system for the solid an Einstein crystal with the same structure [39]. Now the reversible path transforms the original system to an Einstein crystal with fixed center-of-mass, by gradually coupling the atoms to their equilibrium lattice position. For the hard-spherocylinder system the orientation also needs to be coupled to an aligning field. The Hamiltonian that we use to achieve the coupling is the same as given in [26]

where 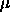and 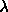are the coupling constants which determine the strength of the harmonic forces. The free energy of the HSC system can be related to the (known) free energy of an Einstein crystal by thermodynamic integration

Here 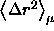is the mean-square displacement and 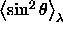the mean square sine of the angle between a particle and the aligning field in a simulation with Hamiltonian 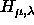. The free energy of the Einstein crystal (with fixed center-of-mass) in the limit of large coupling constants is given by

By performing several simulations at different values of 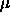and 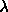one can numerically evaluate the integrals in eqn. 5.4. As the values 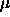and 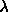at which the integrand is evaluated can be chosen freely, the error in the integration can be minimized by using Gauss-Legendre quadrature. Occurrence of any first order transition was avoided by performing two Gauss-Legendre integrations in succession. 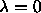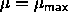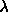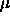The first fixes the positions while leaving , the second aligns all spherocylinders while keeping It is convenient to choose the maximum values of and such that in a simulation at these maximum values, there are essentially no overlaps between the particles. Otherwise it is necessary to correct eqn. 5.5 for the occurrence of overlaps [95].