


Next: Kofke's Gibbs-Duhem integration Up: Free energy calculations Previous: Nematic-smectic free energy



Next: Kofke's Gibbs-Duhem integration
Up: Free energy calculations
Previous: Nematic-smectic free energy
It is not necessary to perform free energy calculations for all values
of 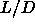 . Once the free energy of a phase at certain density and
. Once the free energy of a phase at certain density and 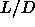 is established the free energy at other values of
is established the free energy at other values of
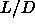 can be obtained by a simple thermodynamic integration scheme.
We can compute the reversible work involved in changing the aspect
ratio of the spherocylinders from
can be obtained by a simple thermodynamic integration scheme.
We can compute the reversible work involved in changing the aspect
ratio of the spherocylinders from 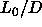 to
to 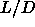 and subsequently
changing the density from
and subsequently
changing the density from 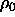 to
to 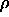 :
:
Here we have set D=1 for convenience.
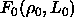 has to be determined by free energy calculations as
described above . The pressure
is obtained from an MD simulation in the usual way, by time averaging the
virial.
has to be determined by free energy calculations as
described above . The pressure
is obtained from an MD simulation in the usual way, by time averaging the
virial.

where 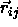 is the vector joining the centers of mass of
particles i and j, and
is the vector joining the centers of mass of
particles i and j, and 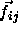 denotes the (impulsive) force on j
due to i.
The derivative
denotes the (impulsive) force on j
due to i.
The derivative 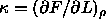 can be
measured at the same time by taking the projection of the
intermolecular force along the particle axis.
can be
measured at the same time by taking the projection of the
intermolecular force along the particle axis.
where 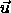 denotes the unit vector of orientation of a particle.
The average
denotes the unit vector of orientation of a particle.
The average  is calculated at constant number density
is calculated at constant number density
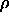 . However, it is more convenient to measure it at constant reduced
density
. However, it is more convenient to measure it at constant reduced
density 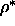 (i.e. at a constant fraction of the close-packing
density). If we denote this derivative by
(i.e. at a constant fraction of the close-packing
density). If we denote this derivative by 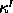 , we get
, we get
and eqn. 5.18 becomes