


Next: The rotator phase Up: Phase diagram for Previous: Phase behavior for



Next: The rotator phase
Up: Phase diagram for
Previous: Phase behavior for
In figure 5.4 the equations of state for spherocylinders with
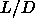 =3 to 5 are displayed.
The reduced pressure is defined as
=3 to 5 are displayed.
The reduced pressure is defined as 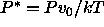 , where
, where 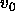 is
the molecular volume of the particle (
is
the molecular volume of the particle (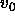 =
= 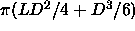 ).
).
We found for 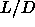 =3 a mechanically stable isotropic, smectic and solid
phase which is in agreement with the results of Veerman and
Frenkel. For
=3 a mechanically stable isotropic, smectic and solid
phase which is in agreement with the results of Veerman and
Frenkel. For 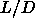 =5 we find also a mechanically stable nematic phase
as was reported by Frenkel,Lekkerkerker and
Stroobants [76].
At values of
=5 we find also a mechanically stable nematic phase
as was reported by Frenkel,Lekkerkerker and
Stroobants [76].
At values of 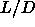 smaller than 5 the nematic
phase region becomes narrower until it disappears when at
smaller than 5 the nematic
phase region becomes narrower until it disappears when at 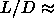 3.5 the isotropic-nematic-smectic triple point is reached.
3.5 the isotropic-nematic-smectic triple point is reached.
Although the isotropic-nematic transition is a first order
transition, the density jump and the hysteresis are too small to
be observed in the simulations, at least for
small 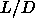 . Only for large values of
. Only for large values of 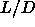 is the density gap
sufficiently large to be observable in our simulations (see
section 5.6).
We therefore estimated the location of the isotropic-nematic
transition for
is the density gap
sufficiently large to be observable in our simulations (see
section 5.6).
We therefore estimated the location of the isotropic-nematic
transition for 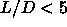 by
measuring the orientational correlation function
by
measuring the orientational correlation function

where 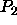 is the second Legendre polynomial and
is the second Legendre polynomial and 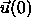 the unit
vector characterizing
the orientation of a particle at the origin while
the unit
vector characterizing
the orientation of a particle at the origin while 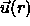 denotes
the orientation of a particle at a distance r from the origin. The
brackets indicate ensemble averaging.
denotes
the orientation of a particle at a distance r from the origin. The
brackets indicate ensemble averaging.
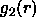 becomes long-ranged at the isotropic-nematic transition and
its limiting value at large r tends to
becomes long-ranged at the isotropic-nematic transition and
its limiting value at large r tends to 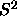 , where S is the
nematic order parameter. Of course, in a periodic system, it is not
meaningful to study correlations at distances larger than half the box
length,
, where S is the
nematic order parameter. Of course, in a periodic system, it is not
meaningful to study correlations at distances larger than half the box
length, 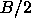 . In figure
5.5 we have plotted the density-dependence of
the nematic order
parameter estimated from the value of
. In figure
5.5 we have plotted the density-dependence of
the nematic order
parameter estimated from the value of 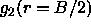 .
At the isotropic-nematic transition there
is a steep increase of S.
The transition densities are summarized in table 5.3.
.
At the isotropic-nematic transition there
is a steep increase of S.
The transition densities are summarized in table 5.3.
| Table: |
Free energy and contributions to the free energy of the smectic
phase. Columns 5 to 10 in the table refer to terms in the rhs of
eqn.
5.15. The maximum values of 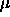 and and
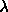 were were 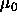 =1000 and =1000 and 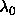 =10000. The number of
particles in the system was 540. The ideal free energy was in all
cases =10000. The number of
particles in the system was 540. The ideal free energy was in all
cases 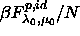 =10.254. =10.254.
|
| Table: |
Free energy and contributions to the free energy of the solid
phase. Columns 6 to 9 in the table refer to terms in the rhs of
eqn.
5.4. The maximum values of 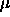 and and
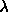 are displayed as well. The number of
particles in the system was 540. are displayed as well. The number of
particles in the system was 540.
|
| Table: |
Contributions to the free energy difference of a nematic phase
at 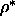 =0.5 and a
the smectic phase at =0.5 and a
the smectic phase at 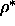 =0.6 for =0.6 for 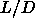 =4.5.
The different integrals in the table refer to terms in the rhs of
eqn.
5.17. The maximum value of =4.5.
The different integrals in the table refer to terms in the rhs of
eqn.
5.17. The maximum value of
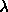 was chosen to be 5. The number of
particles in the system was 600. was chosen to be 5. The number of
particles in the system was 600.
|
Inspection of the equation of state suggest that the nematic to
smectic phase transition is almost continuous
at 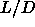 =5, but becomes clearly first order for smaller values of
=5, but becomes clearly first order for smaller values of 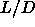 .
A first order smectic-to-solid transition is found for
.
A first order smectic-to-solid transition is found for 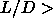 3.1 as can be seen
in figure 5.4.
In order to locate the coexistence curves we used thermodynamic
integration as described in section 5.3.2 to compute
the absolute free energy of the smectic and solid phase and
the free-energy difference between a smectic and a nematic.
The resulting values are displayed in respectively table
5.4,5.5 and 5.6.
Combination of these free energies with the equation of state and
subsequent application of the double tangent construction leads to the
coexisting densities of the nematic to smectic transition, the
smectic solid transition as well as the (meta-stable) solid to isotropic-liquid transition at
3.1 as can be seen
in figure 5.4.
In order to locate the coexistence curves we used thermodynamic
integration as described in section 5.3.2 to compute
the absolute free energy of the smectic and solid phase and
the free-energy difference between a smectic and a nematic.
The resulting values are displayed in respectively table
5.4,5.5 and 5.6.
Combination of these free energies with the equation of state and
subsequent application of the double tangent construction leads to the
coexisting densities of the nematic to smectic transition, the
smectic solid transition as well as the (meta-stable) solid to isotropic-liquid transition at 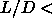 3.5.
The results have been summarized in
table 5.7.
3.5.
The results have been summarized in
table 5.7.
| Table: |
Pressure and densities of coexisting isotropic, nematic and solid
phases for hard spherocylinders with aspect ratios 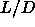 between 3 and
5. Units as in table 5.3. between 3 and
5. Units as in table 5.3. |
The isotropic-smectic-solid triple point is located at 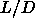 =3.1. The smectic phase is thermodynamically stable at higher
=3.1. The smectic phase is thermodynamically stable at higher 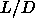 and is separated from the solid and the isotropic liquid by
coexistence regions.
The I-SmA-S triple point occurs at a smaller
and is separated from the solid and the isotropic liquid by
coexistence regions.
The I-SmA-S triple point occurs at a smaller 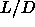 value then the
I-N-SmA triple point. This is not surprising as the smectic phase is
already found to be mechanically stable at
value then the
I-N-SmA triple point. This is not surprising as the smectic phase is
already found to be mechanically stable at 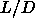 =3 whereas the
nematic phase is not.
=3 whereas the
nematic phase is not.
In their study of the phase diagram of spherocylinders with 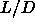 =3 to
=3 to
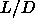 =5, McGrother et al. [27] estimated the isotropic-smectic-solid triple point to
occur at
=5, McGrother et al. [27] estimated the isotropic-smectic-solid triple point to
occur at 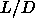 =3.2, followed by an isotropic-nematic-smectic point at
=3.2, followed by an isotropic-nematic-smectic point at
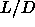 =4. The small disagreement between these numbers and our results
may be due to the fact that their estimates are based on equations of state
obtained by NPT Monte Carlo simulation of spherocylinders in a cubic
box. It is known that the pressure of a smectic can become
anisotropic in a cubic box, resulting in an increase of the free
energy. Moreover, the free energy calculation method used here
is in principle a more reliable method to obtain the phase boundary
than examination of the equation of state. Yet, it should be stressed
that a small error in the free energy will have a noticeable effect on
the estimate of the phase boundaries.
=4. The small disagreement between these numbers and our results
may be due to the fact that their estimates are based on equations of state
obtained by NPT Monte Carlo simulation of spherocylinders in a cubic
box. It is known that the pressure of a smectic can become
anisotropic in a cubic box, resulting in an increase of the free
energy. Moreover, the free energy calculation method used here
is in principle a more reliable method to obtain the phase boundary
than examination of the equation of state. Yet, it should be stressed
that a small error in the free energy will have a noticeable effect on
the estimate of the phase boundaries.
The nematic to smectic phase transition appears to be first order even for 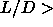 5. This is
rather surprising as in previous simulations this
nematic-smectic transition appeared to be continuous[26].
However, McGrother et al.[27] also found the
nematic-smectic transition at
5. This is
rather surprising as in previous simulations this
nematic-smectic transition appeared to be continuous[26].
However, McGrother et al.[27] also found the
nematic-smectic transition at 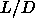 =5 to be first order, albeit with
coexistence densities and pressures that are slightly different from ours. This
minor difference is
probably due to the fact that McGrother et al. did not use free energy
calculations to locate the coexistence curves.
=5 to be first order, albeit with
coexistence densities and pressures that are slightly different from ours. This
minor difference is
probably due to the fact that McGrother et al. did not use free energy
calculations to locate the coexistence curves.
The reduced densities of the coexisting smectic and solid phases are
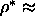 0.66 and
0.66 and 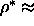 0.68S respectively. These
densities depend only weakly on
0.68S respectively. These
densities depend only weakly on 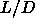 and are effectively constant for
and are effectively constant for 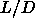 larger than 5.
As the smectic-solid transition is closely related to the freezing of
the quasi-two-dimensional liquid layers, it is interesting to compare
the density where this transition takes place with the freezing density
of hard disks. The quasi-2D in-layer density for the coexisting
smectic and solid phases are
larger than 5.
As the smectic-solid transition is closely related to the freezing of
the quasi-two-dimensional liquid layers, it is interesting to compare
the density where this transition takes place with the freezing density
of hard disks. The quasi-2D in-layer density for the coexisting
smectic and solid phases are
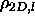 =0.789 and
=0.789 and
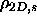 =0.83, respectively.
This should be compared to the most recent estimates of the
solid-liquid coexistence of hard disks
[108]:
=0.83, respectively.
This should be compared to the most recent estimates of the
solid-liquid coexistence of hard disks
[108]: 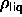 =0.887 and
=0.887 and 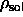 =0.904.
=0.904.


