


Next: Free energy calculations
Up: Simulation techniques
Previous: Simulation techniques
Knowledge of the equation of state often provides a rough estimate of
the limits of stability of the various phases. By starting with
different configurations at different densities the range of
mechanical stability of the observed phase can be estimated. If only one
phase is mechanically stable at a given density, this will also be the
thermodynamically stable phase. If more phases appear to be stable at
the same density, a free-energy calculation is necessary to identify
the one that is thermodynamically stable.
In our simulation studies of the equation of state of hard
spherocylinders, we generated initial conditions both by expansion and
by compression. Specifically, we prepared the configurations
of a (dense) spherocylinder system in the following ways
-
Expansion of a solid phase.
A close packed fcc lattice of spheres with its (111) plane in the xy plane was
stretched in the z-direction by a factor of
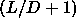 in order to
accommodate a close packed crystal of spherocylinders. This 'ABC'-stacked lattice
was subsequently
expanded to the desired density and allowed to equilibrate.
In the crystalline and smectic phases, the box shape should have the
freedom to fluctuate in order to obtain a isotropic pressure. In those cases,
we used variable-shape constant-volume Monte Carlo (VSMC). Otherwise,
simple constant-volume Monte Carlo was employed.
in order to
accommodate a close packed crystal of spherocylinders. This 'ABC'-stacked lattice
was subsequently
expanded to the desired density and allowed to equilibrate.
In the crystalline and smectic phases, the box shape should have the
freedom to fluctuate in order to obtain a isotropic pressure. In those cases,
we used variable-shape constant-volume Monte Carlo (VSMC). Otherwise,
simple constant-volume Monte Carlo was employed.
-
Compression of an isotropic liquid phase.
At low density an ABC stacked lattice of sphero-cylinders was allowed to melt
into an
isotropic liquid using NVT Monte Carlo. This configuration was subsequently
compressed to the desired density using constant-NPT Monte Carlo and allowed to
equilibrate again with constant-NVT Monte Carlo.
-
Starting from a smectic configuration.
In studying the smectic to nematic transition and the smectic to solid
transition it is preferable to start with a stacking of hexagonal
ordered layers and let this equilibrate by VSMC. The
configuration obtained was subsequently compressed by NPT MC or expanded and
allowed to equilibrate again.
-
Starting from a nematic configuration.
In studying the nematic-smectic transition by compression it is
preferable to start with a defect-free nematic phase. However, the nematic
phase that forms upon compression of the isotropic liquid usually
contains long-lived defects.
To prepare a defect-free nematic phase, we first generated a
hexagonal crystal lattice (``AAA''-stacking)
at a density where
the nematic phase is known to be the stable one.
From this configuration, we first prepare an aligned columnar phase,
by displacing every column in the hexagonal crystal by a random shift
along the z-axis. Subsequently, we allowed the spherocylinders to
rotate but not yet
translate in order to suppress an initial fast relaxation to the
smectic phase. After
a few thousand cycles translation was allowed as well and the
system was allowed to equilibrate. The equilibrated nematic
configuration was compressed by NPT MC to the desired density and
equilibrated again. In principle, we kept the box shape fixed in the
nematic phase. However, close to the smectic phase boundary, where
appreciable smectic fluctuations are already present in the system, we
found it advantageous to use VSMC even in the nematic phase, to speed
up equilibration.
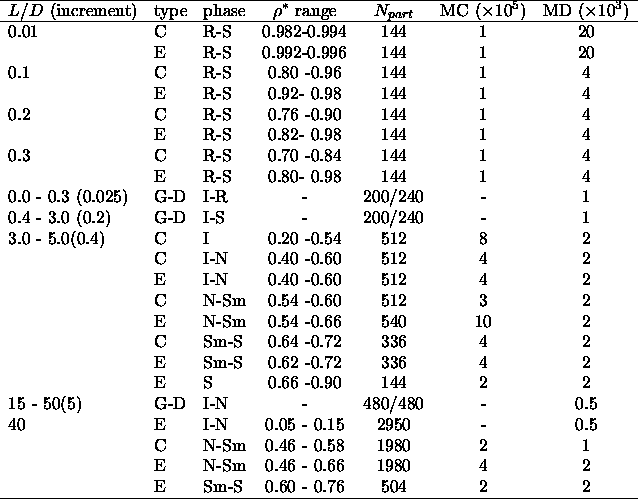
| Table: | Simulation parameters for the various
parts of the phase diagram of hard spherocylinders. In the column
for the type of simulation C stands for compression, E for expansion
and GD for a Gibbs-Duhem integration. In the ``phase'' column I stands for
isotropic, N for nematic,
Sm for smectic, R for rotator and S for solid (ABC) phase. The column
MC gives the total number of Monte Carlo cycles; the column MD the
number of collisions per particle during a MD simulation. Gibbs Duhem
integrations have two numbers at 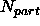 column, because both
phases are simulated simultaneously column, because both
phases are simulated simultaneously |
After preparing well equilibrated configurations of the various
phases, we used Molecular Dynamics simulations to measure the pressure
of the system using the method described in
ref. [105,106]. Occasionally, we also used Molecular
Dynamics to speed up the equilibration. This proved to be particularly
useful near the nematic-smectic
transition where equilibration involves collective rearrangements of
large numbers of particles -- something that is not easily achieved
using single-particle Monte Carlo moves.
Whenever MD simulations are performed, we choose the mass m
of the spherocylinder as our unit of mass, and hence the unit of time
is 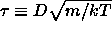 . The moment of inertia was computed,
assuming a uniform mass distribution in the spherocylinder.
The MD simulations that we used to measure the pressure in a
well-equilibrated system were typically of 2000 collisions per
particle.
. The moment of inertia was computed,
assuming a uniform mass distribution in the spherocylinder.
The MD simulations that we used to measure the pressure in a
well-equilibrated system were typically of 2000 collisions per
particle.
The number of particles we used to calculate different parts of the
equation of state and the length of a typical simulation are
summarized in table 5.1.



Next: Free energy calculations
Up: Simulation techniques
Previous: Simulation techniques
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996






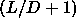 in order to
accommodate a close packed crystal of spherocylinders. This 'ABC'-stacked lattice
was subsequently
expanded to the desired density and allowed to equilibrate.
In the crystalline and smectic phases, the box shape should have the
freedom to fluctuate in order to obtain a isotropic pressure. In those cases,
we used variable-shape constant-volume Monte Carlo (VSMC). Otherwise,
simple constant-volume Monte Carlo was employed.
in order to
accommodate a close packed crystal of spherocylinders. This 'ABC'-stacked lattice
was subsequently
expanded to the desired density and allowed to equilibrate.
In the crystalline and smectic phases, the box shape should have the
freedom to fluctuate in order to obtain a isotropic pressure. In those cases,
we used variable-shape constant-volume Monte Carlo (VSMC). Otherwise,
simple constant-volume Monte Carlo was employed.
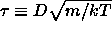 . The moment of inertia was computed,
assuming a uniform mass distribution in the spherocylinder.
The MD simulations that we used to measure the pressure in a
well-equilibrated system were typically of 2000 collisions per
particle.
. The moment of inertia was computed,
assuming a uniform mass distribution in the spherocylinder.
The MD simulations that we used to measure the pressure in a
well-equilibrated system were typically of 2000 collisions per
particle. 

