RESULTS

We prepared a system of 600 cylinders at 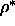=0.8 in an ABC stacking and performed onsager NPT simulations, first expanding to lower densities and subsequently compressing. The equation of state of spherocylinders in the limit 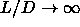is shown in figure 5.15. There is no isotropic phase at finite reduced densities because the I-N transition has shifted down to 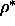=0. Therefore, at all reduced densities below 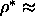0.47 the nematic phase is stable. 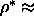The nematic to smectic transition is estimated to take place at 0.47. This is in agreement with the predictions of Poniewierski who located the N-S transition at 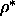=0.46 using bifurcation analysis [112].

At higher density the smectic phase will be thermodynamically stable, until at 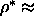0.66 the system crystallizes in an AAA stacking. This transition is first order as is clear from the strong hysteresis at 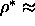0.66 in figure 5.15. The system prefers an AAA stacking because the particles are hindered by fewer particles in the neighboring layers than in an AB or ABC stacking and hence have more entropy. The AAA phase will undergo a transition to an ABC crystal only at close packing, because the ABC stacked lattice will be stabilized only if the distance between layers is of the order of D. At that point the particles start to feel the hemispheres of the particles in the neighboring layers. 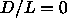Because this can only happen at close packing densities.

We also found evidence for a columnar structure between the smectic and the AAA phase. This columnar phase appeared meta-stable with respect to the AAA crystal.