Next: Shifted periodic boundaries Up: What is the Previous: What is the
Next: Shifted periodic boundaries
Up: What is the
Previous: What is the
The hysteresis at densities
around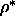 
=0.5 between the compression and expansion
branch in figure 5.15 is an indication for a first order N-S transition.
When we consider the nematic order
parameter of the system, this hysteresis becomes even more clear. In the limit 
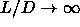the
nematic order parameter can be written to leading order in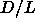 
as
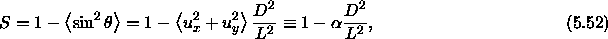
where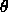 
is the angle the particles make with the director and
the latter equation defines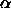 
as the mean square shift of the cylinders.
In figure 5.16 we plotted the measured value of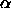 
as a function of the reduced density for both the
compression and expansion branches. The most remarkable feature is
that near the transition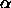 
is larger in the smectic phase than
in the nematic. This corresponds to a more orientational ordered
nematic at lower densities and a less ordered smectic at higher
density. There is a competition between translational and
orientational entropy. In the nematic phase the translational entropy
is large but the rods are restricted in their rotations. On the other hand,
in the smectic phase, the layering increases the orientational entropy, which manifests itself as herringbone fluctuations of the smectic layers.
Figure 5.16 also clearly shows the hysteresis between the
compression and expansion branches. The compression
from the nematic phase shows only increasing disorder for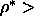 
0.54 whereas 
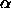in the case of the expansion from the smectic
drops to low value below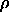 
=0.5.
The two examples of hysteresis given above suggests that we
have a first order transition.
However, as before, only free energy calculations can locate the exact
transition. We performed free energy difference calculations as
described in section 5.3.2.4 to estimate the free energy
difference between an nematic Onsager system at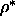 
=0.4 and a
smectic at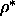 
=0.5. Those calculations did not result in
reasonable values for the nematic smectic coexistence densities.
in an Onsager spherocylinder system as a function of reduced
density 
for a compression from the nematic (filled circles)
and a expansion from the smectic phase (open circles). Note the clear
hysteresis.