Next: Phase behavior for Up: Phase diagram for Previous: Phase diagram for
Next: Phase behavior for
Up: Phase diagram for
Previous: Phase diagram for
For hard spherocylinders with lengths shorter than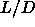 
= 3 there is
only a fluid phase and, at high densities, a crystalline
phase. For rods with 
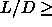0.35, the crystalline phase is an
orientationally ordered (hexagonal) lattice.
Below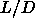 
=0.35 we find that a face-centered cubic
``rotator'' phase becomes stable (see section 5.5).
Gibbs-Duhem simulations were performed to locate
transition from isotropic fluid to the fcc plastic crystal
the in the range
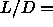0 to 0.3. As a reference point, we used
the coexistence properties of the hard-sphere model (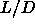
=0) [56].
In the region 0.4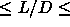
3, we used
the free energy data of ref [26] at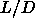 
=1 as our fixed
reference point. As a test, we checked that the computed coexistence
curve did reproduce results of ref. [26] for the
densities of the coexisting phases for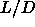 
=3.
The results of the Gibbs-Duhem integration are given in
table 5.2 and are displayed in figure 5.1. The
coexistence curves are smooth and the densities reproduce the earlier
values for
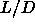=3 to within a few tenth of a percent. The solid density at
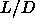=2.4 is slightly off, presumably because the solid
happened to contain a defect.
In any event,
as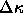 
(in eqn.
5.26) is evaluated as the (small) difference between two large,
fluctuating numbers,
it is difficult to obtain this quantity with high accuracy.
An additional problem is that it takes a long time before the
simulation box for the solid phase has relaxed to its equilibrium
shape (i.e. the one that makes the pressure tensor isotropic).
The Gibbs Duhem integration results for the fluid-rotator transition
for 0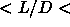
0.3 can be compared with Monte Carlo simulations of the
fluid-plastic crystal coexistence in hard dumbbell systems, performed
by Singer and Mumaugh [107]. Figure 5.3 shows the
fluid-rotator coexistence region of the spherocylinders in combination
with the results on dumbbells. As one would expect, the agreement is
excellent because spherocylinder hardly differ from dumbbells in this
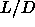region.
We found that Gibbs-Duhem integration could not be used in the region
between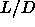 
=0.3 and 
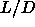=0.4 where three phases (liquid, plastic
solid and ordered solid) compete.
On basis of the available data we estimate that the
liquid-solid-solid triple point is located around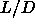 
=0.35 and
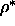=0.75.
0.3 and
the Monte Carlo simulation results of Singer and Mumaugh (triangles) for dumbbells of small 
between 3 and 5. The pressure is expressed in
the dimensionless unit 
, where 
is the molecular volume of
the spherocylinders. The dashed curves correspond to a compression
whereas the solid curves denote an expansion. The different
mechanically stable phases are indicated.
(see text) for hard spherocylinders with 
between 3.4
and 4.6. The solid curve corresponds to an expansion
branch, the dashed curve to a compression branch