KOFKE'S GIBBS-DUHEM INTEGRATION

The location of a fluid-solid coexistence curve can be determined by performing several free-energy calculations and measurements of the equation-of-state for a large number of 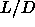values. However, this approach is computationally rather expensive. To avoid this problem, we use a modification of a method that was recently developed by Kofke to trace coexistence curves [84]. The advantage of this method is that only equation-of-state information at the coexistence curve is required to follow the 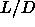-dependence of the melting curve. In its original form, the Kofke scheme is based on the Clapeyron equation which describes the temperature-dependence of the pressure at which two phases coexist (see section 4.3):

where 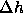is the molar enthalpy difference and 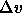the molar volume difference of the two phases. This equation is not self starting, in the sense that one point on the coexistence curve must be known before the rest of the curve can be computed by integration of eqn. 5.23. Kofke refers to this method as ``Gibbs-Duhem'' integration.

In the present case, we are not interested in the temperature dependence of the coexistence curve (this dependence is trivial for hard-core systems), but in the dependence of the coexistence pressure on 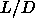, the length-to-width ratio of the spherocylinders. In order to obtain a Clapeyron-like equation relating the coexistence pressure to 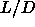, we should first write down the explicit dependence of the (Gibbs) free energy of the system on :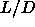

where is the derivative 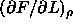defined in eqn. 5.20 and where we have used the fact that D is our unit of length. Along the coexistence curve, the difference in chemical potential of the two phases is always equal to zero. Hence,

where 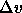is the difference in molar volume of the two phases at coexistence and 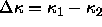. From eqn. 5.25 we can immediately deduce the equivalent of the Clausius-Clapeyron equation

Kofke used a predictor-corrector scheme to integrate eqn. 5.23. However, we find that this integration scheme, when applied to eqn. 5.26, is not very stable. In particular, when the predicted pressure is slightly off, the predictor-corrector scheme leads to unphysical oscillations. We therefore introduce a slightly different integration procedure. Instead of calculating one new point in the phase diagram every step, we start with a set of simulations at different L values and pressure for both phases. The derivatives are calculated according to eqn. 5.26 and subsequently fitted to a polynomial in L

This polynomial is integrated to give new pressures which are used in the next iteration. The old and new pressures are mixed together to improve the stability. This procedure is repeated until convergence of the pressure has occurred. The set of starting values are obtained by application of the original Gibbs-Duhem scheme.

In Kofke's application of the Gibbs-Duhem method, the MC simulations are carried out in the isothermal-isobaric (NPT) ensemble. However, in the present case (hard-core particles), it is more efficient to use Molecular Dynamics to compute the derivative . In practice, we use a hybrid approach where MD simulations are embedded in a constant NPT-MC scheme. True constant-pressure MD is not an attractive option for hard-core models.