


Next: Simulation techniques Up: Brief summary of Previous: Phase diagram for



Next: Simulation techniques
Up: Brief summary of
Previous: Phase diagram for
In figure 5.2, the phase behavior for long rods is
depicted as a function of 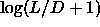 to give equal emphasis to the
different parts of the phase diagram.
For larger values of
to give equal emphasis to the
different parts of the phase diagram.
For larger values of 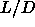 , the I-N transition moves to lower
densities and the density jump at the I-N transition, which is too
small to be measured for rods with
, the I-N transition moves to lower
densities and the density jump at the I-N transition, which is too
small to be measured for rods with 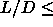 5, increases to almost
20%, as
5, increases to almost
20%, as 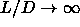 , as predicted by Onsager theory. In
contrast, the density of
the nematic-smectic transition is not very sensitive to the
length-to-width ratio of the rods and approaches the finite
limit
, as predicted by Onsager theory. In
contrast, the density of
the nematic-smectic transition is not very sensitive to the
length-to-width ratio of the rods and approaches the finite
limit 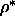 =0.47 as
=0.47 as 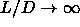 .
Similarly, the smectic-to-solid
transition exhibits only a weak dependence on
.
Similarly, the smectic-to-solid
transition exhibits only a weak dependence on 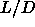 and occurs still at
and occurs still at
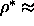 0.66 in the
0.66 in the 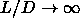 limit .
limit .
At 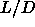 values greater than approximately 7 a crystal phase with an 'AAA'
stacking becomes
stable between the smectic and the ABC stacked solid. This crystal
phase is characterized by hexagonal planes which are stacked
precisely on top of each other.
At higher density the ABC stacked solid, which has the hexagonal planes shifted with respect to each other, will still be the most stable
structure. The density of the AAA-ABC transition increases quickly for
values greater than approximately 7 a crystal phase with an 'AAA'
stacking becomes
stable between the smectic and the ABC stacked solid. This crystal
phase is characterized by hexagonal planes which are stacked
precisely on top of each other.
At higher density the ABC stacked solid, which has the hexagonal planes shifted with respect to each other, will still be the most stable
structure. The density of the AAA-ABC transition increases quickly for
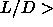 7 to reach the close packing limit at
7 to reach the close packing limit at 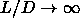 .
.
More details on the phase behavior of long spherocylinders can be found in section 5.6.