Next: Phase diagram in Up: The rotator phase Previous: Finite densities
Next: Phase diagram in
Up: The rotator phase
Previous: Finite densities
The rotator solid transition is expected to be first order even in the
limit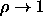 
and 
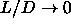. We cannot
access this region using ordinary simulation methods.
However, somewhat surprisingly, it is possible to perform simulation
in this limit and get useful information about the limiting behavior
of the solid-solid transition.
To see how this is achieved, let us first consider the case where
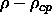and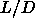 
are both small but
finite. In the dense solid phase, the particles are constrained to
move in the vicinity of their lattice positions and we can safely
ignore diffusion. Therefore, we only
have to take the deviations from the lattice positions into account.
The overlap criterion of two spherocylinders i and j is based on
the shortest distance between the two cylinder axes with orientation
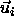and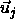 
(see [77])
where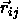 
is the shortest distance vector, 
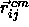is the center-of-mass separation of neighboring particles j
an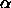d 
and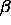 
are the distances along
the axis of the two particles from the center of mass to the point
of closest approach.
In a dense solid, we can rewrite the center-of-mass separation as the vector
sum of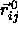 
, the distance between the lattice positions of
i and j, and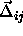 
, the difference of the vector
displacements of particles i and j from their lattice positions. Hence,
It is important to realize that, in the limit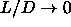 
, all
spherocylinder contacts will involve only the spherical
end-caps. Moreover, near close packing, the relative particle displacements
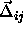will become negligible compared to the lattice vectors
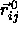. In this limit, the vector distance of closest approach
between two spherocylinders will therefore be parallel to the lattice vector
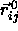. We need therefore only consider the component of
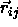along the direction of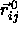 
It is most convenient to express the lattice vectors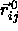 
in terms of the unit vectors 
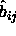that denote the
directions of nearest neighbor bonds in the undistorted fcc
lattice. In that lattice, the lattice vector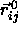 
can be
written as
In the close-packed spherocylinder crystal, the lattice is expanded
along the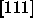 
-axis by an amount 
.
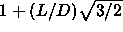If we consider a crystal near (but not at) close packing, the crystal
will expand in all three directions, but not necessarily
isotropically. We assume that this expansion does not change the
symmetry of the lattice -- i.e. if we define the alignment direction
of the spherocylinders (the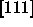 
direction) to be the z-axis,
then we assume that the expanded crystal can be generated from the
close packed crystal by isotropic expansion in the xy-plane plus a
(different) expansion along the z-axis.
It is convenient to express the lattice vectors
of the expanded lattice as follows
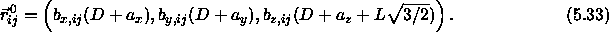
Note that, as we consider the limit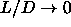 
and
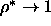, L and 
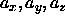are much smaller than D.
Because of the assumed symmetry in the xy-plane,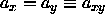 
. We denote the average value of 
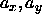and
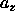by a. It is related to the expansion of the lattice
If we define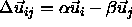 
the absolute shortest distance becomes
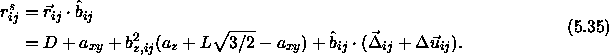
As the spherocylinders can only touch with their spherical end-caps, the surface-to-surface distance is given by
where, in the last line, we have used the values for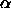 
and
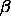appropriate for the distance
between spherical end-caps. The spherocylinder overlap criterion in the
limit
, 
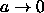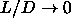is simply
It turns out to be more convenient to express all distances in units
of a. The density enters the problem through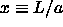 
. We
can now perform a Monte Carlo simulation of this model by setting up
an undistorted fcc lattice with
unit nearest neighbor distances and move a randomly selected
sphero-cylinder i from its initial scaled displacement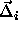 
and orientation 
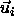to a trial displacement and orientation in such
a way that microscopic reversibility is satisfied. We use the
conventional Metropolis rule to accept or reject the trial move.
The system is anisotropic and we must allow box shape fluctuations to
ensure equilibrium. In the simulation the box shape is determined by
the ratio of
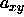and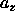 
.
During trial moves that change the shape of the simulation box, the
total volume should stay constant. Equation 5.34 then implies
that the changes in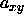 
and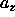 
are related by
The conventional Metropolis criterion is used to decide on the acceptance of shape-changing trial moves. To speed up equilibration, we also used Molecular Dynamics simulations of the close-packed spherocylinder model. The MD scheme that we use is essentially identical to the one used in off-lattice simulations[105,106]. All the distances are scaled with a factor a. In the scaled space the new overlap criterion of eqn. 5.36 is used to locate colliding pairs. The virial expression for the pressure in the close-packing limit is
where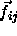 
denotes the rate of momentum transfer between
sphero-cylinders i and j and the last line defines the quantity
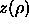that is measured in the simulations.
Simulations were performed both by compression from ``low'' density
(i.e. low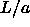 
) and by expansion from ``high'' density (high 
).
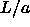The free energy of both the rotator and the aligned phases were
calculated by Einstein integration as discussed in the previous
chapter. It should be noted that the free energies of both phases do
in fact diverge at close packing. However the free energy difference is finite, and this is what we need to compute the phase
coexistence.
In order to see how this can be achieved, consider the expression for
the free energy of a (fixed center-of-mass) Einstein crystal in the
limit of close packing. Every particle in the hard-spherocylinder
crystal is confined to move within a cell with average radius a.
We wish to switch on an Einstein spring constant that is sufficiently
large to suppress hard-core overlaps. This can only be achieved if the
spring-constant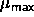 
in eqn.
5.5 is of order
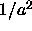. Hence, we expect 
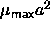to be finite. It is
therefore convenient to write the free energy of the Einstein crystal
as follows
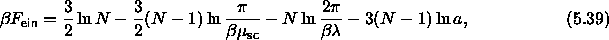
where we have defined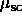 
as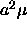 
. Note that
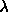, the ``orientational'' spring constant remains finite.
The expression for the free energy of the spherocylinder crystal
(eqn.
5.4) now becomes
The computational scheme is essentially the same as with the
conventional Einstein crystal method.
The main difference is that all displacements in eqn.
5.40
are expressed in
units of a. The scaled coupling constant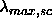 
remains
finite. All divergences are now contained in the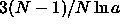 
term.
When searching for the point of phase coexistence, we need to be able
to compute the variation of the free energy with density.
The free energy at any value of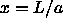 
is obtained by thermodynamic
integration starting from the density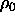 
where the direct
free-energy calculation has been performed
It is more convenient to change to the integration variable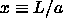 
, which is related to the density through 
.
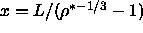In the MD simulations we do not measure the pressure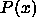 
but rather 
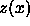(see eqn.
5.38).
The variation of the Helmholtz free energy with x can be written as
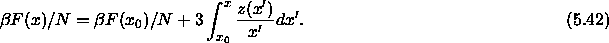
At coexistence the pressure in both phases is equal.
Using eqn.
5.38 and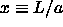 
, it
is straightforward to show that the condition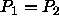 
can be
written as
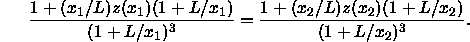
To leading order in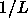 
this implies that
The chemical potential is given by
The condition for equilibrium,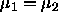 
corresponds to
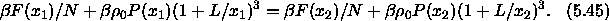
All terms in this equation diverge in the close-packing
limit. However, all differences remain finite. This is immediately
obvious for the terms involving the pressure as, at coexistence,
= 
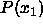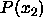. We recall that the free energy diverges as
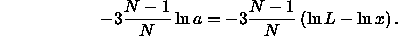
We can therefore write the Helmholtz free energy of the crystal as a
non-diverging part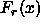 
, where the subscript r stands for regular, and the diverging remainder
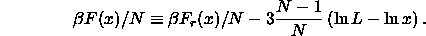
The condition for the equality of the chemical potential now becomes
where we have dropped the terms that cancel on the left and right hand
side and where we have ignored terms that vanish in the limit
.
| Figure: | Scaled equations of state for hard
spherocylinder solids in the
limit 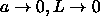 (see
eqn.
5.43). The dotted curve denotes a compression
and the solid curve corresponds to an expansion |
| Table: | Regular part of the Helmholtz free energy per particle in the close packed limit. The values have been obtained by Einstein integration. |
Figure 5.8 shows the ``equation of state''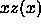 
for
the dense plastic crystal and ordered solid.
The free energies of the reference systems are given in table
5.10. The coexistence values of x, pressure and
chemical potential that follow from equations 5.43 and
5.46 are
where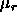 
, is the regular part of the chemical potential, given by
eqn.
5.46.
As x is defined as the ratio of L and a, eqn.
5.47
describes the initial (small L) dependence of the plastic-ordered
transition on the spherocylinder length.
As presented, a given value of x corresponds to a slope of the
coexistence curve in the L,a plane.
However, by using the definition of x,
every value of x corresponds to a curve in the
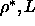plane.
The resulting solid-solid coexistence curves are plotted
in figure 5.7. It is interesting to note that,
even at 
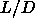as large as 0.3,
the slope of rotator-solid coexistence curve
is still
dominated by the behavior at close packing
