CONCLUSION

  In summary, we have mapped out the spherocylinder phase diagram over a wide range of densities and 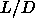values, such that it was possible to establish the link with the hard-sphere phase diagram for small 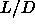and with the Onsager limit for 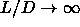. We find that the liquid crystalline nematic phase is stable from about 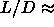3.5. The isotropic nematic coexistence decreases as a function of 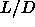and follows the Onsager theory in the 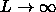limit.
The smectic phase becomes stable at 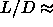3.1. The isotropic-smectic and later on the nematic-smectic transition starts off as a strong first-order transition for 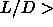3.5 . The density jump becomes smaller at highe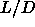r . For 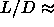7 the AAA stacked crystalline phase becomes stable. The AAA-ABC transition was found to be first order. The transition density increases with 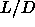and reaches close packing in the Onsager limit. Between 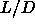=4 and 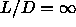the first order smectic-solid transition is located at the almost constant reduced densities 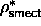=0.66 and 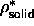=0.68.

We determined the phase behavior of spherocylinders in the Onsager limit and estimated the location of nematic to smectic phase at 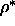=0.47 which in agreement with the predicted value of 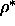=0.46. In order to establish the link between the Onsager limit and the phase behavior for finite spherocylinders we plotted in figure 5.19 the phase diagram as a function of .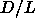
The rotator to solid phase transition at low 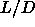was calculated and appeared to be strongly dominated by the behavior in the close-packed limit.
In the calculations we used three non-standard simulation techniques:

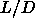• The Gibbs-Duhem integration method of Kofke was modified to compute the -dependence of phase-coexistence curves.
• The plastic-rotator transition was investigated in the close packing limit by mapping the system onto a special lattice model.
• The Onsager limit was studied by scaling the infinitely long particles to finite length.