Next: The AAA crystal Up: Phase diagram in Previous: Numerical Techniques
Next: The AAA crystal
Up: Phase diagram in
Previous: Numerical Techniques
The results of the Gibbs-Duhem integration of the long rods are shown in table 5.11 and the coexistence densities are plotted in figure 5.10. The Gibbs ensemble results are displayed in table 5.12. As can be seen, the results of both methods agree quite well.
In figure 5.11 we have re-plotted the phase diagram in a way that makes comparison with the Onsager limit easier. In particular, we now use as our density variable
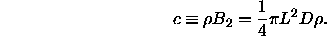
In these units the coexistence densities remain finite in
the Onsager limit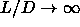 
.
In order to facilitate the extrapolation to the Onsager limit, we use
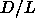rather than 
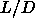as the variable characterizing the aspect
ratio of the rods. Figure 5.11 shows that the I-N
coexistence curves extrapolate nicely to the Onsager limit at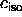 
=3.29 and 
=4.19 [110], except for a few points on
the nematic coexistence curve at high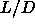 
. Apparently, at these high
lengths it is difficult to equilibrate the nematic phase completely.
It is clear from figure 5.11 that already for rods
with an aspect ratio less than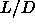 
=20 (or 
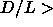0.05), the Onsager
limit dominates
the phase behavior. This result is not at all obvious as, for rods
with this length, the Onsager assumption that all higher virial
coefficients are negligible is not yet satisfied [111].
Yet, we cannot rule out the possibility that the discrepancy at
higher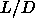 
(lower 
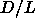) is an effect of higher virial coefficients. The agreement at
lower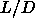 
values should then be attributed to a fortuitous
cancellation of errors.
| Figure: | Equation of state
for spherocylinders with aspect ratio 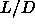 =40.The dashed curves correspond to a compression
whereas the solid curves denote an expansion. The different
mechanically stable phases are indicated. All units as in
figure 5.4. |
Of course, the nematic to smectic and smectic to solid transition are
more difficult to study, because they
occur at higher density. This has two consequences: first of all,
higher density means more particles in a box of a given (minimum)
size, and secondly equilibration at high densities is slower.
For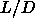 
=40 the equation-of-state is plotted in figure
5.12.
We estimate that the reduced densities of the coexisting smectic and
solid phases are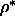 
=0.66 and 
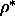=0.68 respectively. The
nematic-smectic transition is estimated to take place at about
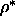=0.5. However, it is difficult to locate this transition
accurately, as the smectic
fluctuations in the nematic phase decay extremely slowly, even at
lower densities. Poniewierski [112] has studied the nematic to
smectic transition in the Onsager limit using bifurcation analysis. He
found that the bifurcation point of the nematic-smectic transition is
located at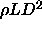 
=0.531 which corresponds to a reduced density
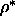=0.46. This agrees with the decreasing trend in the
transition density if one goes from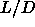 
=5 to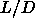 
=40. However,
it also shows that the N-SmA transition for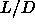 
=40 is significantly
different from the transition at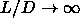 
.
In figure 5.2 we have combined our results for the phase
behavior at large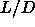 
values with the low 
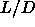phase diagram
discussed before. In order to give equal
emphasis to all parts of the phase diagram, we have plotted the
figure in the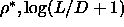 
plane.
