chapter 5
 section 5.1
section 5.1
Intuitively, one associates increased order with a decrease in
entropy. It is therefore surprising that a large number of phase
transitions exist in which both the structural order and the entropy
of the system increase. In particular, all ordering transitions in
systems of particles that have exclusively hard-core interactions, are
of this type. Already in the forties, Onsager showed [25]
that thin hard rods must form a nematic liquid crystal at sufficiently
high densities. In the fifties, the computer-simulation studies of Alder
and Wainwright, and Wood and Jacobson [92,93] provided the
first conclusive evidence that hard spherical particles undergo a
first order freezing transition.
Subsequently, computer simulations of a variety of models of
non-spherical hard-core models showed that excluded volume effects
could not only account for the stability of
nematics [94,95] but also for the existence of
smectic [96,97,76,26] and
columnar [98,99] liquid-crystalline phases (for
a review, see [77]).
As already mentioned, simulations of hard
particles are of considerable practical relevance for the
study of colloidal materials consisting of anisometric inorganic
colloids [17] or rodlike virus
particles [100]. To a first approximation, hard
sphero-cylinders (cylinders of length L and diameter D capped with two
hemispheres at both ends) provide a good model for rodlike colloidal particles
with short-ranged repulsive interactions. The parameter that
characterizes the phase behavior of such particles is the
length-to-width ratio 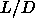 . Of course, the behavior of real rodlike
colloids may differ from that of rigid hard spherocylinders, either
because the colloid-colloid interaction is not truly a hard-core
repulsion or because real colloids are never completely rigid. It is
clearly of interest to know where the analogy between real colloids
and the corresponding hard-core model breaks down. However, in order
to detect such differences in behavior, it is obviously important to
have a good knowledge of the hard-spherocylinder (HSC) phase diagram
over a wide range of
. Of course, the behavior of real rodlike
colloids may differ from that of rigid hard spherocylinders, either
because the colloid-colloid interaction is not truly a hard-core
repulsion or because real colloids are never completely rigid. It is
clearly of interest to know where the analogy between real colloids
and the corresponding hard-core model breaks down. However, in order
to detect such differences in behavior, it is obviously important to
have a good knowledge of the hard-spherocylinder (HSC) phase diagram
over a wide range of 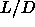 values.
values.
A first attempt to map out the HSC phase diagram was reported by
Veerman and Frenkel [26]. However, this study focused on
only a small number of rather widely spaced 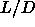 values. As a
consequence, the phase boundaries for intermediate
values. As a
consequence, the phase boundaries for intermediate 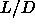 values could
only be sketched, while some phase boundaries were not studied at all.
This situation is clearly unsatisfactory, as the HSC system is now
often used as a reference system to compare both with experiment and
with theory. For precisely this reason, McGrother et
al. [27] recently
performed more extensive simulations in the region 3
values could
only be sketched, while some phase boundaries were not studied at all.
This situation is clearly unsatisfactory, as the HSC system is now
often used as a reference system to compare both with experiment and
with theory. For precisely this reason, McGrother et
al. [27] recently
performed more extensive simulations in the region 3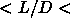 5.
The aim of the present study is to compute the complete phase
diagram of the spherocylinder model (i.e. from
5.
The aim of the present study is to compute the complete phase
diagram of the spherocylinder model (i.e. from 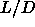 =0 to
=0 to
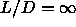 , and from low-density to close packing.
In order to achieve this, we employ several
computational techniques that have been developed in the past few
years that enable us to map the HSC phase diagram over a wide
range of
, and from low-density to close packing.
In order to achieve this, we employ several
computational techniques that have been developed in the past few
years that enable us to map the HSC phase diagram over a wide
range of 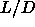 values.
values.
In this study we pay special attention to three aspects of the
phase diagram. The first is the location of the orientational
order-disorder transition in the solid (for small anisometries). This
transition has, thus far, not been studied for spherocylinders. More
interestingly, using the novel computational technique from
section 3.2.4 and [101],
we are now able to trace the coexistence curve between rotator phase
and orientationally ordered crystal all the way to close packing.
Second, we are interested in the behavior of spherocylinders for large
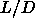 and in particular the Onsager limit.
The third point of special interest is the location of the triple
points in the phase diagram. Specifically, there is a maximum
and in particular the Onsager limit.
The third point of special interest is the location of the triple
points in the phase diagram. Specifically, there is a maximum 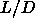 value beyond which no crystalline rotator phase can exist and
similarly, there are lower limits for
value beyond which no crystalline rotator phase can exist and
similarly, there are lower limits for 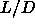 below which the smectic-A,
nematic and the crystalline AAA phases become thermodynamically unstable.
below which the smectic-A,
nematic and the crystalline AAA phases become thermodynamically unstable.
Veerman and Frenkel [26] made no attempt to estimate the
first triple point and could only give rather wide margins for the
other three. In particular, they found that whereas rods with a
length-to-width ratio 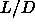 =5 can form both a stable nematic
and a stable smectic phase, at
=5 can form both a stable nematic
and a stable smectic phase, at 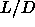 =3
the smectic phase is only meta-stable while the nematic phase is even
mechanically unstable. Clearly, the only conclusion that could be
drawn from the simulations in ref. [26] is that the
triple points that terminate the range
of nematic and smectic stability must be located somewhere between
=3
the smectic phase is only meta-stable while the nematic phase is even
mechanically unstable. Clearly, the only conclusion that could be
drawn from the simulations in ref. [26] is that the
triple points that terminate the range
of nematic and smectic stability must be located somewhere between
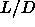 =3 and
=3 and 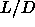 =5. But it remained unclear where exactly this would
happen and which triple point would come first.
=5. But it remained unclear where exactly this would
happen and which triple point would come first.
Moreover, one should expect the nematic-smectic transition to be
be first order for small 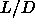 values and continuous for long
sphero-cylinders. Different theories make different predictions about
the location of the tricritical point:
in refs. [102,103] is estimated that the tricritical point
corresponds to
values and continuous for long
sphero-cylinders. Different theories make different predictions about
the location of the tricritical point:
in refs. [102,103] is estimated that the tricritical point
corresponds to 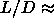 5 while the theoretical analysis in
ref [104] suggest that it should occur at
5 while the theoretical analysis in
ref [104] suggest that it should occur at 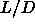 =50.
The present simulations strongly suggest that this tri-critical
point occurs at an
=50.
The present simulations strongly suggest that this tri-critical
point occurs at an 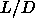 values appreciable larger than 5 , but are
not suited to determine the exact location of
the tri-critical point.
values appreciable larger than 5 , but are
not suited to determine the exact location of
the tri-critical point.
The recent NPT Monte Carlo simulations of McGrother et
al.[27] were performed on a system of spherocylinders with 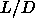 range 3 to
5. They found that the isotropic-smectic-A-solid triple point occurs at
range 3 to
5. They found that the isotropic-smectic-A-solid triple point occurs at 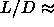 3.2 and that the isotropic-nematic-smectic triple point is
located around
3.2 and that the isotropic-nematic-smectic triple point is
located around 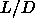 =4. Further they also found evidence for a first
order nematic-smectic transition at
=4. Further they also found evidence for a first
order nematic-smectic transition at 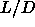 =5.
=5.
The outline of the remainder of this chapter is as follows.
For readers who are less interested in the technical details of
the simulations, section 5.2 summarizes the main
results concerning the phase behavior of spherocylinders. Subsequently,
different aspects of the simulations are discussed in some
detail. Section 5.3 describes the simulation techniques and the methods we used to calculate the free energy of the
different phases.
In particular, section 5.3.3 describes how we have modified
the Gibbs-Duhem integration technique of Kofke [84]
to trace the melting curve for 0.4 3.
The results for
3.
The results for 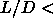 5 are presented in section 5.4.
The location of the first order transition between solid and rotator is
discussed in section 5.5. This section also describes
the computational technique used to study this transition in the limit
of close packing of the spherocylinders.
In section 5.6 results for long rods (up to
5 are presented in section 5.4.
The location of the first order transition between solid and rotator is
discussed in section 5.5. This section also describes
the computational technique used to study this transition in the limit
of close packing of the spherocylinders.
In section 5.6 results for long rods (up to
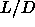 =60) are presented. The
isotropic-nematic transition is studied both by Gibbs-ensemble
simulation and Gibbs-Duhem integration. For
=60) are presented. The
isotropic-nematic transition is studied both by Gibbs-ensemble
simulation and Gibbs-Duhem integration. For 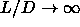 this transition is expected to approach the behavior predicted by the
Onsager theory. We discuss the
nematic-smectic and smectic-solid transitions for long rods
(
this transition is expected to approach the behavior predicted by the
Onsager theory. We discuss the
nematic-smectic and smectic-solid transitions for long rods
(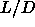 =40). We also present a rough estimate for the AAA phase
boundaries in this section. Finally, in section 5.7 the
simulation of spherocylinders in the limit
=40). We also present a rough estimate for the AAA phase
boundaries in this section. Finally, in section 5.7 the
simulation of spherocylinders in the limit 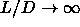 are discussed.
are discussed.
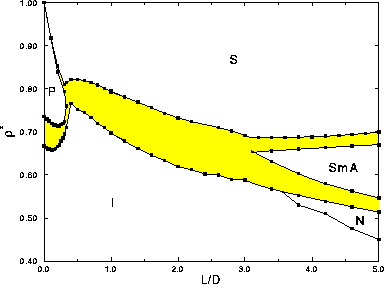
| Figure: | Phase diagram for hard spherocylinders of aspect
ratio 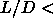 5. All two-phase regions are shown shaded. In the
figure, the following phases can be distinguished: the low-density
isotropic liquid, the high-density orientationally-ordered solid, the
low- 5. All two-phase regions are shown shaded. In the
figure, the following phases can be distinguished: the low-density
isotropic liquid, the high-density orientationally-ordered solid, the
low-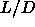 plastic solid and, for plastic solid and, for 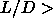 3.5, the nematic and smectic-A phases 3.5, the nematic and smectic-A phases |
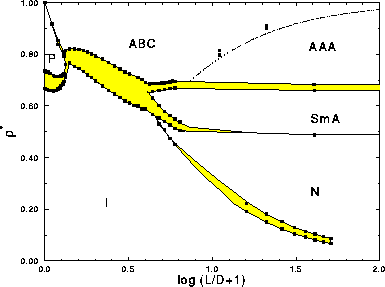
| Figure: | Summary of the phase diagram of hard
spherocylinders with 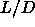 between 0 and 60. In order to give equal
emphasis to all parts of the phase diagram, we have plotted between 0 and 60. In order to give equal
emphasis to all parts of the phase diagram, we have plotted
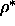 as a function of as a function of 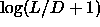 . The dashed line is a crude
estimate for the
first order AAA-ABC transition as given in eqn.
5.51. . The dashed line is a crude
estimate for the
first order AAA-ABC transition as given in eqn.
5.51. |
chapter 5
 section 5.1
section 5.1
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
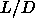 . Of course, the behavior of real rodlike
colloids may differ from that of rigid hard spherocylinders, either
because the colloid-colloid interaction is not truly a hard-core
repulsion or because real colloids are never completely rigid. It is
clearly of interest to know where the analogy between real colloids
and the corresponding hard-core model breaks down. However, in order
to detect such differences in behavior, it is obviously important to
have a good knowledge of the hard-spherocylinder (HSC) phase diagram
over a wide range of
. Of course, the behavior of real rodlike
colloids may differ from that of rigid hard spherocylinders, either
because the colloid-colloid interaction is not truly a hard-core
repulsion or because real colloids are never completely rigid. It is
clearly of interest to know where the analogy between real colloids
and the corresponding hard-core model breaks down. However, in order
to detect such differences in behavior, it is obviously important to
have a good knowledge of the hard-spherocylinder (HSC) phase diagram
over a wide range of 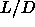 values.
values.
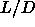 values. As a
consequence, the phase boundaries for intermediate
values. As a
consequence, the phase boundaries for intermediate 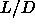 values could
only be sketched, while some phase boundaries were not studied at all.
This situation is clearly unsatisfactory, as the HSC system is now
often used as a reference system to compare both with experiment and
with theory. For precisely this reason, McGrother et
al. [
values could
only be sketched, while some phase boundaries were not studied at all.
This situation is clearly unsatisfactory, as the HSC system is now
often used as a reference system to compare both with experiment and
with theory. For precisely this reason, McGrother et
al. [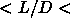 5.
The aim of the present study is to compute the complete phase
diagram of the spherocylinder model (i.e. from
5.
The aim of the present study is to compute the complete phase
diagram of the spherocylinder model (i.e. from 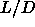 =0 to
=0 to
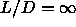 , and from low-density to close packing.
In order to achieve this, we employ several
computational techniques that have been developed in the past few
years that enable us to map the HSC phase diagram over a wide
range of
, and from low-density to close packing.
In order to achieve this, we employ several
computational techniques that have been developed in the past few
years that enable us to map the HSC phase diagram over a wide
range of 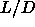 values.
values.
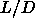 and in particular the Onsager limit.
The third point of special interest is the location of the triple
points in the phase diagram. Specifically, there is a maximum
and in particular the Onsager limit.
The third point of special interest is the location of the triple
points in the phase diagram. Specifically, there is a maximum 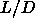 value beyond which no crystalline rotator phase can exist and
similarly, there are lower limits for
value beyond which no crystalline rotator phase can exist and
similarly, there are lower limits for 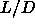 below which the smectic-A,
nematic and the crystalline AAA phases become thermodynamically unstable.
below which the smectic-A,
nematic and the crystalline AAA phases become thermodynamically unstable.
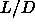 =5 can form both a stable nematic
and a stable smectic phase, at
=5 can form both a stable nematic
and a stable smectic phase, at 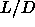 =3
the smectic phase is only meta-stable while the nematic phase is even
mechanically unstable. Clearly, the only conclusion that could be
drawn from the simulations in ref. [
=3
the smectic phase is only meta-stable while the nematic phase is even
mechanically unstable. Clearly, the only conclusion that could be
drawn from the simulations in ref. [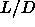 =3 and
=3 and 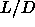 =5. But it remained unclear where exactly this would
happen and which triple point would come first.
=5. But it remained unclear where exactly this would
happen and which triple point would come first.
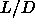 values and continuous for long
sphero-cylinders. Different theories make different predictions about
the location of the tricritical point:
in refs. [
values and continuous for long
sphero-cylinders. Different theories make different predictions about
the location of the tricritical point:
in refs. [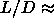 5 while the theoretical analysis in
ref [
5 while the theoretical analysis in
ref [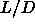 =50.
The present simulations strongly suggest that this tri-critical
point occurs at an
=50.
The present simulations strongly suggest that this tri-critical
point occurs at an 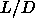 values appreciable larger than 5 , but are
not suited to determine the exact location of
the tri-critical point.
values appreciable larger than 5 , but are
not suited to determine the exact location of
the tri-critical point.
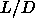 range 3 to
5. They found that the isotropic-smectic-A-solid triple point occurs at
range 3 to
5. They found that the isotropic-smectic-A-solid triple point occurs at 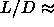 3.2 and that the isotropic-nematic-smectic triple point is
located around
3.2 and that the isotropic-nematic-smectic triple point is
located around 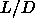 =4. Further they also found evidence for a first
order nematic-smectic transition at
=4. Further they also found evidence for a first
order nematic-smectic transition at 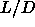 =5.
=5.
 3.
The results for
3.
The results for 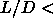 5 are presented in section
5 are presented in section 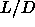 =60) are presented. The
isotropic-nematic transition is studied both by Gibbs-ensemble
simulation and Gibbs-Duhem integration. For
=60) are presented. The
isotropic-nematic transition is studied both by Gibbs-ensemble
simulation and Gibbs-Duhem integration. For 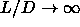 this transition is expected to approach the behavior predicted by the
Onsager theory. We discuss the
nematic-smectic and smectic-solid transitions for long rods
(
this transition is expected to approach the behavior predicted by the
Onsager theory. We discuss the
nematic-smectic and smectic-solid transitions for long rods
(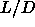 =40). We also present a rough estimate for the AAA phase
boundaries in this section. Finally, in section
=40). We also present a rough estimate for the AAA phase
boundaries in this section. Finally, in section 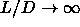 are discussed.
are discussed.

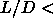 5. All two-phase regions are shown shaded. In the
figure, the following phases can be distinguished: the low-density
isotropic liquid, the high-density orientationally-ordered solid, the
low-
5. All two-phase regions are shown shaded. In the
figure, the following phases can be distinguished: the low-density
isotropic liquid, the high-density orientationally-ordered solid, the
low-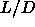 plastic solid and, for
plastic solid and, for 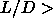 3.5, the nematic and smectic-A phases
3.5, the nematic and smectic-A phases
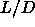 between 0 and 60. In order to give equal
emphasis to all parts of the phase diagram, we have plotted
between 0 and 60. In order to give equal
emphasis to all parts of the phase diagram, we have plotted
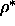 as a function of
as a function of 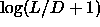 . The dashed line is a crude
estimate for the
first order AAA-ABC transition as given in eqn.
. The dashed line is a crude
estimate for the
first order AAA-ABC transition as given in eqn.