In the Asakura-Oosawa model, the colloids are represented by hard spheres of diameter
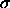 , while the polymers are assumed to be
spheres of diameter
, while the polymers are assumed to be
spheres of diameter 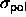 that are mutually interpenetrable, yet cannot penetrate the colloidal particles.
As a consequence, every colloidal particle excludes a sphere of volume
that are mutually interpenetrable, yet cannot penetrate the colloidal particles.
As a consequence, every colloidal particle excludes a sphere of volume 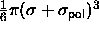 to the polymers.
When two colloidal particles are brought together, these spherical volumes will overlap and the volume accessible to the polymer will increase. It is this increase in free volume that causes an effective attraction and the eventual phase separation of the colloids. Recent computer simulations of polymer-colloid mixtures [10] indicate that the Asakura-Oosawa model is quite realistic if
to the polymers.
When two colloidal particles are brought together, these spherical volumes will overlap and the volume accessible to the polymer will increase. It is this increase in free volume that causes an effective attraction and the eventual phase separation of the colloids. Recent computer simulations of polymer-colloid mixtures [10] indicate that the Asakura-Oosawa model is quite realistic if 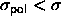 .
.Of course, the above mechanism for polymer-colloid phase separation is more general: spherical colloids and globular polymers are just the simplest example. In this chapter, we focus on another limiting example, namely a mixture of spherical colloids and thin rodlike polymers. In the limit that the polymers are infinitely thin, this mixture is expected to resemble the Asakura-Oosawa model, because the polymer-polymer excluded volume vanishes, while the polymer colloid excluded volume is a spherocylinder with a length to width ratio
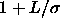 , where L is the length of the rodlike polymers. As in the case of the flexible polymer-colloid mixture the free volume for the rodlike polymer can be increased by clustering of the colloids.
One would therefore expect to see phase separation in such mixtures.
However, although a light-scattering study of a mixture of colloids and fairly rigid rod-like polymers was reported by Tracy et al. [28], phase separation was not observed.
, where L is the length of the rodlike polymers. As in the case of the flexible polymer-colloid mixture the free volume for the rodlike polymer can be increased by clustering of the colloids.
One would therefore expect to see phase separation in such mixtures.
However, although a light-scattering study of a mixture of colloids and fairly rigid rod-like polymers was reported by Tracy et al. [28], phase separation was not observed.In this chapter we report a systematic numerical study of mixtures of hard-sphere colloids with thin rodlike polymers of varying length. The aim of the study is threefold: first of all, we wish to establish if there is indeed a fluid-fluid phase separation in this mixture. This is not a-priori obvious because both the spheres and the rodlike polymers are convex bodies. The existence of a fluid-fluid phase separation in the simplest mixture of convex bodies, viz. hard spheres, continues to be a matter of speculation [29,30]. For other mixtures of convex bodies, firm data are lacking. A second aim of the study is to provide a guide for experiments: we intend to indicate under what conditions (colloid density, polymer fugacity,
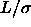 ratio) phase transitions are to be expected. We shall consider both the possibility of fluid-fluid and fluid-solid transitions.
Finally, we wish to verify if the theoretical description of
polymer-colloid mixtures discussed in ref [21] and section 1.8 can be generalized to rodlike polymers.
ratio) phase transitions are to be expected. We shall consider both the possibility of fluid-fluid and fluid-solid transitions.
Finally, we wish to verify if the theoretical description of
polymer-colloid mixtures discussed in ref [21] and section 1.8 can be generalized to rodlike polymers.In our numerical study of possible fluid-fluid coexistence, we have made use of the Gibbs-ensemble method of Panagiotopoulos [31,32,33]. However, as will be explained below, a naive implementation of this scheme is extremely inefficient in the present case. We have therefore generalized the Gibbs-ensemble method to perform multi-particle exchanges, where the configurational-bias Monte Carlo method [34] is used to achieve a high acceptance probability of trial moves. This simulation scheme is described in section 2.2.1. In section 2.2.2 we present the simulation results of the fluid-fluid demixing. The solid-liquid coexistence is discussed in section 2.2.3. The application of first-order perturbation theory to the mixture is described in section 2.3.1, followed by a discussion of the limiting case of infinitely long rods,
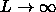 . In
section 2.3.3 we compare the simulation results with the
theory.
. In
section 2.3.3 we compare the simulation results with the
theory.