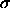 in a volume V and in osmotic equilibrium with a
reservoir containing an ideal gas of rods
of length L at a fugacity
in a volume V and in osmotic equilibrium with a
reservoir containing an ideal gas of rods
of length L at a fugacity 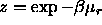 , where
, where 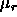 is
the chemical potential of the rods, is approximated by
is
the chemical potential of the rods, is approximated by
To compute the fluid-fluid coexistence curves of the rod-sphere mixture we used the perturbation theory approach developed by Lekkerkerker et al. [21,30] and discussed in detail in chapter 1.
In this approach, the grand potential of a system of N hard spheres with
diameter 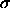 in a volume V and in osmotic equilibrium with a
reservoir containing an ideal gas of rods
of length L at a fugacity
in a volume V and in osmotic equilibrium with a
reservoir containing an ideal gas of rods
of length L at a fugacity 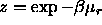 , where
, where 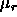 is
the chemical potential of the rods, is approximated by
is
the chemical potential of the rods, is approximated by

Here 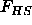 is the free energy of the hard spheres, which only
depends on the density
is the free energy of the hard spheres, which only
depends on the density 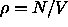 and
and 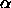 is the average
fraction of the total volume available for a rod.
is the average
fraction of the total volume available for a rod.
To calculate the phase equilibria, one needs the pressure and the
chemical potential 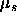 of the spheres
of the spheres
For the pressure of the hard sphere reference system 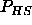 we use the Carnahan-Starling equation of state
we use the Carnahan-Starling equation of state

where 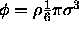 is the volume fraction of hard spheres. The chemical potential of the hard sphere fluid can be obtained from the standard thermodynamic relations.
For the free volume fraction
is the volume fraction of hard spheres. The chemical potential of the hard sphere fluid can be obtained from the standard thermodynamic relations.
For the free volume fraction 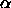 one can use the scaled particle theory for one rod in a solution of spheres [40]
one can use the scaled particle theory for one rod in a solution of spheres [40]
This is an underestimation of the chemical potential, therefore an overestimation of the free volume as we already saw in figure 2.2. Nevertheless, it turns out that this equation gives quite accurate results as we shall see in section 3.3.
Substitution of eqn.
2.17 in eqn.
2.14 and eqn.
2.15 yields explicit expressions for the pressure and chemical potential in terms of the volume fractions in phase I and phase II. The coexistence curves were obtained by equating the pressure and chemical potentials in both phases.