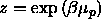 , where
, where 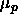 is the polymer chemical potential.
As we are imposing the fugacity of the system , the proper
thermodynamic quantity is the grand canonical partition function
is the polymer chemical potential.
As we are imposing the fugacity of the system , the proper
thermodynamic quantity is the grand canonical partition function
In this section we describe the thermodynamic treatment of the
polymer-colloid mixture within the AO model developed by Lekkerkerker et al. [21]. This approach
is analogous to the derivation of the potential of mean force
discussed in section 1.5. We consider a
system of N colloidal particles dispersed in a polymer solution, in a
volume V. This system is in osmotic equilibrium with a large reservoir
containing only a polymer solution, at fixed fugacity 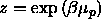 , where
, where 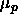 is the polymer chemical potential.
As we are imposing the fugacity of the system , the proper
thermodynamic quantity is the grand canonical partition function
is the polymer chemical potential.
As we are imposing the fugacity of the system , the proper
thermodynamic quantity is the grand canonical partition function
where 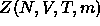 is the canonical partition function of a system of N
colloid and m polymers. As the AO-model states that the bare colloid-colloid
interaction
is the canonical partition function of a system of N
colloid and m polymers. As the AO-model states that the bare colloid-colloid
interaction 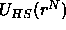 is a hard sphere potential that does not depend on the presence of the
polymers, we can write
is a hard sphere potential that does not depend on the presence of the
polymers, we can write
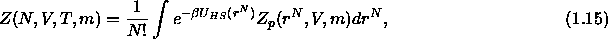
where 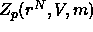 is the canonical partition function of the
polymers in a particular configuration of the colloidal
particles. As the polymers were assumed not to interact with each other in this model,
is the canonical partition function of the
polymers in a particular configuration of the colloidal
particles. As the polymers were assumed not to interact with each other in this model, 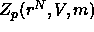 can be expressed as the mth power of the
one polymer partition function which is in turn equal to the free volume
available to a polymer
can be expressed as the mth power of the
one polymer partition function which is in turn equal to the free volume
available to a polymer
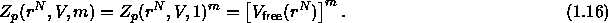
The integration over the translational degrees of freedom of the polymer yields the free volume, i.e. that part of the volume that is not excluded to the polymers by the hard-core colloids. The grand canonical partition function of eqn. 1.14 now becomes
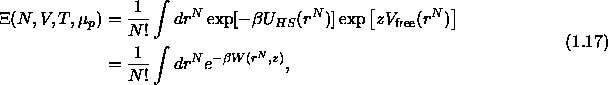
where 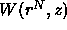 is again the potential of mean force but now due to the
presence of the polymer
is again the potential of mean force but now due to the
presence of the polymer
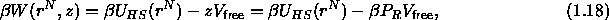
where 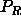 is the osmotic pressure of the polymers in the
reservoir (we have used the fact that, for ideal polymers, the (osmotic)
pressure and the fugacity are identical).
is the osmotic pressure of the polymers in the
reservoir (we have used the fact that, for ideal polymers, the (osmotic)
pressure and the fugacity are identical).
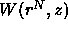 can be interpreted as an effective potential. If the
displacement of a colloidal particle decreases the free volume
available to the polymers, then
can be interpreted as an effective potential. If the
displacement of a colloidal particle decreases the free volume
available to the polymers, then 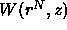 increases (i.e. becomes more
repulsive). This potential is of purely entropic origin because we
have assumed only hard-core interactions. Up to this point,
the derivation
has been exact (at least, in the context of the AO model).
However,
increases (i.e. becomes more
repulsive). This potential is of purely entropic origin because we
have assumed only hard-core interactions. Up to this point,
the derivation
has been exact (at least, in the context of the AO model).
However, 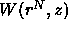 is a many-body potential because the free volume
is a many-body potential because the free volume
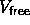 depends not just on binary but also on multiple overlap of
depletion zones. This complicates the theoretical description of the
free volume and it is usually necessary to introduce approximations at
some level. However, no such approximations are needed in the
numerical simulation of the depletion interaction. Hence, simulations
can be used to test the validity of the approximations used in the theory.
depends not just on binary but also on multiple overlap of
depletion zones. This complicates the theoretical description of the
free volume and it is usually necessary to introduce approximations at
some level. However, no such approximations are needed in the
numerical simulation of the depletion interaction. Hence, simulations
can be used to test the validity of the approximations used in the theory.
The simplest theoretical approximation of the depletion interaction is
based on thermodynamic perturbation theory. We replace
 ) by its average value in the corresponding
hard-spheres reference system. This yields the following approximation
for the grand potential
) by its average value in the corresponding
hard-spheres reference system. This yields the following approximation
for the grand potential
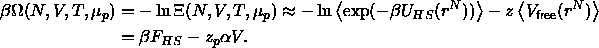
Here the brackets stand for an ensemble average over the colloid
configurations, 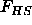 is the free energy of the hard spheres, which
only depends on the density
is the free energy of the hard spheres, which
only depends on the density 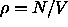 and
and 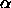 is the average
fraction of the total volume available for a polymers.
is the average
fraction of the total volume available for a polymers.
From the grand potential one can calculate the osmotic pressure P and the
chemical potential 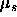 of the colloidal spheres
of the colloidal spheres
Together with expressions for the Helmholtz free energy 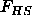 and
for the available free volume fraction
and
for the available free volume fraction 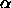 these equations can be
used for a theoretical study of the phase behavior of a
colloid-polymer mixture. The above formalism is also applicable
to hard colloidal particles with non-spherical shapes, provided that
we use the appropriate expression for F and
these equations can be
used for a theoretical study of the phase behavior of a
colloid-polymer mixture. The above formalism is also applicable
to hard colloidal particles with non-spherical shapes, provided that
we use the appropriate expression for F and 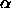 .
.