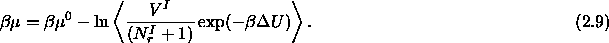chapter 2
 section 2.2
section 2.2
 subsection 2.2.1
subsection 2.2.1
To calculate the phase equilibria directly, we use the Gibbs-Ensemble Monte Carlo simulation
approach developed by Panagiotopoulos [31,32]. In this method, the coexisting phases are simulated in parallel. 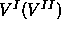 denotes the volume of the periodic box containing phase
denotes the volume of the periodic box containing phase 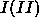 . The total volume is denoted by V. The number of spheres and rods in either box is
denoted by
. The total volume is denoted by V. The number of spheres and rods in either box is
denoted by 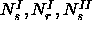 and
and 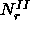 .
.
During the simulation ordinary MC displacement steps are performed in both phases and occasionally particles and volume are exchanged between the boxes to maintain respectively chemical and mechanical equilibrium.
The particle moves inside a box are accepted according to the conventional Metropolis scheme. For trial moves to change the volume, we follow the procedure described in ref. [33].
The exchange rules are slightly more complicated.
The rods can be exchanged without any difficulty and we can use the usual acceptance rule for moving a rod from box I to II:
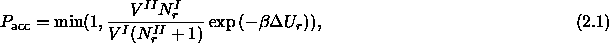
where 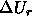 is the change in potential energy upon exchange of a
rod.
is the change in potential energy upon exchange of a
rod.
The spheres however, cannot be exchanged directly because the insertion probability in both phases will be very low due to the presence of rods. Nearly always a sphere will overlap with one or more needles. To overcome this we can make use of the Configurational Bias Monte Carlo scheme originally derived by Biben [35] who in turn based it on a scheme suggested in ref. [34].
The procedure is as follows. First one tries to move a sphere from one box to the other. When the sphere overlaps with any other sphere the trial move is rejected.
Otherwise, rods overlapping with the sphere in its new position are removed and are randomly inserted into the former box in such a way that they would have intersected the sphere in its original position. This procedure creates a bias in the sampling. In the following we show how to correct for this bias.
Before discussing particle exchange between two boxes, we focus on a scheme for moving particles within the same box. Suppose we want to swap a sphere with the overlapping needles on the new position. The acceptance rule for this step is governed by detailed balance:

Here  is the probability to generate and
is the probability to generate and 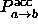 the probability to accept the move from configuration a to configuration b.
the probability to accept the move from configuration a to configuration b. 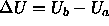 is the potential energy difference between a and b.
To satisfy the detailed balance condition one can use the Metropolis scheme with the acceptance rule
is the potential energy difference between a and b.
To satisfy the detailed balance condition one can use the Metropolis scheme with the acceptance rule

In normal simulations  , the chance of generating configuration a is equal to
, the chance of generating configuration a is equal to  . In the present case the generating probabilities depend on the volume, the number of particles and the specific configuration. If we try to move n rods starting from configuration a, the probability to generate a certain configuration b is given by
. In the present case the generating probabilities depend on the volume, the number of particles and the specific configuration. If we try to move n rods starting from configuration a, the probability to generate a certain configuration b is given by

where 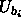 denotes the energy of the
denotes the energy of the 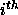 moved rod in configuration b, the weight factor
moved rod in configuration b, the weight factor 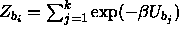 plays the role of the single rod partition function. Once we have moved a sphere, we try to move the overlapping rods into the old position of the sphere. For each of the n overlapping rods the weight factor is calculated by inserting rods k times randomly in the overlap volume of the rod and the moved sphere.
plays the role of the single rod partition function. Once we have moved a sphere, we try to move the overlapping rods into the old position of the sphere. For each of the n overlapping rods the weight factor is calculated by inserting rods k times randomly in the overlap volume of the rod and the moved sphere.
Using eqn.
2.2 - eqn.
2.4 and the relation 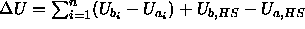 the acceptance probability becomes,
the acceptance probability becomes,

where 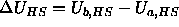 takes into account the interaction of the moved sphere with all other spheres and
takes into account the interaction of the moved sphere with all other spheres and 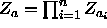 for configuration a. For convenience, it is assumed that the number of trial insertions k is the same in both
for configuration a. For convenience, it is assumed that the number of trial insertions k is the same in both 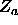 and
and 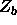 ,
The weight factors
,
The weight factors 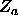 and
and 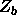 of the old and the new situation respectively, must be calculated. Notice that besides the moved sphere the only difference between a and b are the position of the n overlapping rods, so we only need to calculate the weight factors for those rods.
of the old and the new situation respectively, must be calculated. Notice that besides the moved sphere the only difference between a and b are the position of the n overlapping rods, so we only need to calculate the weight factors for those rods.
The above scheme is valid for a move within one box. In the Gibbs-Ensemble scheme the situation is somewhat different. Suppose we want to move a sphere from box II to I. The overlapping n needles in box I in situation a are moved to box II. The probability to generate the new configuration b is now given by

where the factor 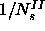 is the probability to pick one of the spheres in box II and the volume factor is due to the random choice of the sphere position in box I. The product in eqn.
2.6 gives the probability to move n rods between boxes and is the same as in eqn.
2.4.
For the reverse move,
is the probability to pick one of the spheres in box II and the volume factor is due to the random choice of the sphere position in box I. The product in eqn.
2.6 gives the probability to move n rods between boxes and is the same as in eqn.
2.4.
For the reverse move,  can be written as
can be written as

where the additional 1 in the first factor arises because in the reverse move one extra sphere can be chosen.
Using 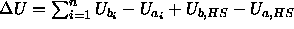 and the definition of the weight factor Z, the total probability of accepting a sphere exchange from box II to I is:
and the definition of the weight factor Z, the total probability of accepting a sphere exchange from box II to I is:
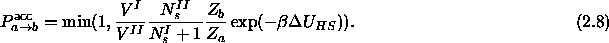
Note that the number of rods does not occur in this acceptance rule, because the rods cannot be chosen freely once a particular sphere has been randomly selected.
At first sight it seems strange that the acceptance rule does not contain the number of displaced rods. In the limit in which the rods shrink to ideal point particles, however, it is immediately clear that the thermodynamics of the hard sphere fluid cannot depend on the configurations of an ideal gas.
The calculation of the 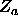 and
and 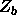 is as follows.
The orientation of the rod to be inserted is chosen randomly and it is placed within the overlap volume of the rod and the sphere. This is repeated k times.
is as follows.
The orientation of the rod to be inserted is chosen randomly and it is placed within the overlap volume of the rod and the sphere. This is repeated k times. 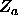 and
and 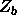 are equal to the number of times the rod does not overlap with another sphere in the old configuration a respectively in the new situation b.
are equal to the number of times the rod does not overlap with another sphere in the old configuration a respectively in the new situation b.
To check chemical equilibrium one may want to know the chemical potential of the rods.
The chemical potential of the rods is measured by the Widom insertion method which is slightly altered due to the Gibbs-ensemble [33].
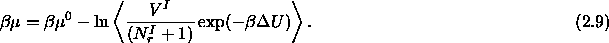
With the above steps it is possible to calculate phase equilibria in
rod sphere mixtures directly.
chapter 2
 section 2.2
section 2.2
 subsection 2.2.1
subsection 2.2.1
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
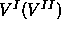 denotes the volume of the periodic box containing phase
denotes the volume of the periodic box containing phase 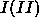 . The total volume is denoted by V. The number of spheres and rods in either box is
denoted by
. The total volume is denoted by V. The number of spheres and rods in either box is
denoted by 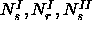 and
and 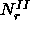 .
.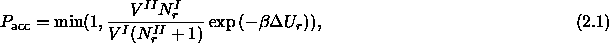
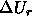 is the change in potential energy upon exchange of a
rod.
is the change in potential energy upon exchange of a
rod.
 is the probability to generate and
is the probability to generate and 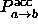 the probability to accept the move from configuration a to configuration b.
the probability to accept the move from configuration a to configuration b. 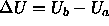 is the potential energy difference between a and b.
To satisfy the detailed balance condition one can use the Metropolis scheme with the acceptance rule
is the potential energy difference between a and b.
To satisfy the detailed balance condition one can use the Metropolis scheme with the acceptance rule

 , the chance of generating configuration a is equal to
, the chance of generating configuration a is equal to  . In the present case the generating probabilities depend on the volume, the number of particles and the specific configuration. If we try to move n rods starting from configuration a, the probability to generate a certain configuration b is given by
. In the present case the generating probabilities depend on the volume, the number of particles and the specific configuration. If we try to move n rods starting from configuration a, the probability to generate a certain configuration b is given by

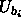 denotes the energy of the
denotes the energy of the 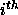 moved rod in configuration b, the weight factor
moved rod in configuration b, the weight factor 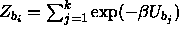 plays the role of the single rod partition function. Once we have moved a sphere, we try to move the overlapping rods into the old position of the sphere. For each of the n overlapping rods the weight factor is calculated by inserting rods k times randomly in the overlap volume of the rod and the moved sphere.
plays the role of the single rod partition function. Once we have moved a sphere, we try to move the overlapping rods into the old position of the sphere. For each of the n overlapping rods the weight factor is calculated by inserting rods k times randomly in the overlap volume of the rod and the moved sphere.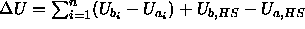 the acceptance probability becomes,
the acceptance probability becomes,

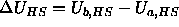 takes into account the interaction of the moved sphere with all other spheres and
takes into account the interaction of the moved sphere with all other spheres and 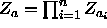 for configuration a. For convenience, it is assumed that the number of trial insertions k is the same in both
for configuration a. For convenience, it is assumed that the number of trial insertions k is the same in both 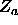 and
and 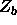 ,
The weight factors
,
The weight factors 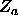 and
and 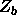 of the old and the new situation respectively, must be calculated. Notice that besides the moved sphere the only difference between a and b are the position of the n overlapping rods, so we only need to calculate the weight factors for those rods.
of the old and the new situation respectively, must be calculated. Notice that besides the moved sphere the only difference between a and b are the position of the n overlapping rods, so we only need to calculate the weight factors for those rods.
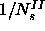 is the probability to pick one of the spheres in box II and the volume factor is due to the random choice of the sphere position in box I. The product in eqn.
is the probability to pick one of the spheres in box II and the volume factor is due to the random choice of the sphere position in box I. The product in eqn.
 can be written as
can be written as

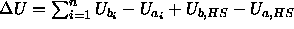 and the definition of the weight factor Z, the total probability of accepting a sphere exchange from box II to I is:
and the definition of the weight factor Z, the total probability of accepting a sphere exchange from box II to I is:
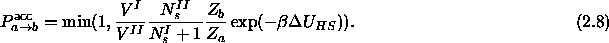
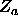 and
and 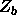 is as follows.
The orientation of the rod to be inserted is chosen randomly and it is placed within the overlap volume of the rod and the sphere. This is repeated k times.
is as follows.
The orientation of the rod to be inserted is chosen randomly and it is placed within the overlap volume of the rod and the sphere. This is repeated k times. 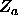 and
and 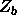 are equal to the number of times the rod does not overlap with another sphere in the old configuration a respectively in the new situation b.
are equal to the number of times the rod does not overlap with another sphere in the old configuration a respectively in the new situation b.