chapter 2
 section 2.2
section 2.2
 subsection 2.2.2
subsection 2.2.2
In the model studied in our simulations the colloidal particles are represented by hard spheres with a diameter 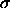 while the rodlike particles are modeled by infinitely thin needles of length L. As these needles are infinitely thin, their mutual excluded volume vanishes. However the needles cannot intersect with the hard core colloidal particles.
while the rodlike particles are modeled by infinitely thin needles of length L. As these needles are infinitely thin, their mutual excluded volume vanishes. However the needles cannot intersect with the hard core colloidal particles.
In order to establish fluid-fluid phase separation we performed
modified Gibbs-ensemble Monte Carlo simulations for rod lengths
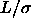 =2, 3, 4, 5, 6 at different fugacities.
The overall starting density of colloidal particles in the two boxes was
=2, 3, 4, 5, 6 at different fugacities.
The overall starting density of colloidal particles in the two boxes was 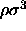 =0.25 which located the system in a two phase region of the phase diagram.
=0.25 which located the system in a two phase region of the phase diagram.
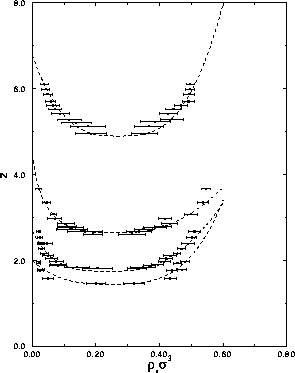
| Figure: | Coexistence curves for mixtures of hard spheres and rods. On the x-axis the number density of hard spheres is set out. The fugacity of the rods, z, is plotted versus the reduced number density of hard spheres, 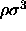 .
The data points refer to the Gibbs-Ensemble results. From top to
bottom the sets of points denote the binodals for .
The data points refer to the Gibbs-Ensemble results. From top to
bottom the sets of points denote the binodals for 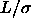 =2,3,4 and
5. The dashed curves are fits to eqn.
2.10 with an exponent =2,3,4 and
5. The dashed curves are fits to eqn.
2.10 with an exponent 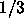 . . |
The total number of spheres in the system was 110. We did not fix the number of rodlike polymers, but rather kept their fugacity z fixed.
During the simulations the number of rods varied from 100 to 1000.
As a test, we measured the chemical potential of the needles and the spheres using Widoms particle insertion technique [36] during a simulation. The chemical potential 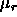 of the rods is directly related to the fugacity by
of the rods is directly related to the fugacity by 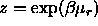 . We checked that the actual chemical potentials of the two species remained constant in both phases.
. We checked that the actual chemical potentials of the two species remained constant in both phases.
For equilibration of every system 10,000 MC cycles were executed, whereas 20,000 cycles were performed for data collection. During a cycle every particle on average was moved once. In addition the average cycle contained 80 attempted particle exchanges and 1 volume exchange between the two phases.
The maximum step sizes of the particle moves were adjusted in order to keep the acceptance probability around 30 - 40 %. The acceptance probability of hard sphere exchanges which involved the Configurational Bias Monte Carlo step was 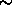 5%. This means that on average during every cycle 2 % of the total number of particles was exchanged. The acceptance probability for the exchange of the needles was
5%. This means that on average during every cycle 2 % of the total number of particles was exchanged. The acceptance probability for the exchange of the needles was 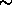 40%.
40%.
Figure 2.1 shows the fluid-fluid coexistence curves obtained in the Gibbs-ensemble simulations.
As the length of the needles is increased, the coexistence curves shift to lower fugacity. This is to be expected because the range of the depletion interaction increases with length. Therefore, fewer rods are needed to induce the phase separation.
Because of the analogy between this phase separation and the liquid-vapor coexistence in simple fluids we expect that the shape of the coexistence curve in the neighborhood of the critical point is given by the scaling form

where  is the density difference between the dense and the dilute phase and we assumed
is the density difference between the dense and the dilute phase and we assumed 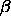 =0.33, the usual 3D Ising critical exponent. From these simulations it is not possible to obtain a good estimate of the actual critical exponent.
The dashed curves shown in figure 2.1 are fits of the scaling form (2.10).
=0.33, the usual 3D Ising critical exponent. From these simulations it is not possible to obtain a good estimate of the actual critical exponent.
The dashed curves shown in figure 2.1 are fits of the scaling form (2.10).
The critical density shifts to lower values and the coexistence curves
become more asymmetrical with increasing needle length. In the case of very long rods every sphere will be expelled from the dilute vapor like phase, which causes the critical density to go asymptotically to zero for 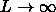 . This limit will be discussed in more detail in section 3.2.
. This limit will be discussed in more detail in section 3.2.
chapter 2
 section 2.2
section 2.2
 subsection 2.2.2
subsection 2.2.2
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
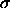 while the rodlike particles are modeled by infinitely thin needles of length L. As these needles are infinitely thin, their mutual excluded volume vanishes. However the needles cannot intersect with the hard core colloidal particles.
while the rodlike particles are modeled by infinitely thin needles of length L. As these needles are infinitely thin, their mutual excluded volume vanishes. However the needles cannot intersect with the hard core colloidal particles. 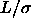 =2, 3, 4, 5, 6 at different fugacities.
The overall starting density of colloidal particles in the two boxes was
=2, 3, 4, 5, 6 at different fugacities.
The overall starting density of colloidal particles in the two boxes was 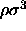 =0.25 which located the system in a two phase region of the phase diagram.
=0.25 which located the system in a two phase region of the phase diagram.

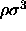 .
The data points refer to the Gibbs-Ensemble results. From top to
bottom the sets of points denote the binodals for
.
The data points refer to the Gibbs-Ensemble results. From top to
bottom the sets of points denote the binodals for 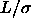 =2,3,4 and
5. The dashed curves are fits to eqn.
=2,3,4 and
5. The dashed curves are fits to eqn.
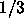 .
.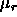 of the rods is directly related to the fugacity by
of the rods is directly related to the fugacity by 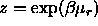 . We checked that the actual chemical potentials of the two species remained constant in both phases.
. We checked that the actual chemical potentials of the two species remained constant in both phases. 5%. This means that on average during every cycle 2 % of the total number of particles was exchanged. The acceptance probability for the exchange of the needles was
5%. This means that on average during every cycle 2 % of the total number of particles was exchanged. The acceptance probability for the exchange of the needles was  40%.
40%.
 is the density difference between the dense and the dilute phase and we assumed
is the density difference between the dense and the dilute phase and we assumed 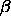 =0.33, the usual 3D Ising critical exponent. From these simulations it is not possible to obtain a good estimate of the actual critical exponent.
The dashed curves shown in figure
=0.33, the usual 3D Ising critical exponent. From these simulations it is not possible to obtain a good estimate of the actual critical exponent.
The dashed curves shown in figure 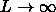 . This limit will be discussed in more detail in section 3.2.
. This limit will be discussed in more detail in section 3.2.