section 2.3
subsection 2.3.3 section 2.3
subsection 2.3.3
In figure 2.3 the binodal curves from first order perturbation theory are compared with the Gibbs-ensemble results. The critical points are well predicted for small length but become worse for longer rods. Because there is no adjustable parameter in the model, the accuracy of the theoretical curves is surprising. This good agreement is probably due to the accuracy of the SPT expression for the free volume eqn.
2.15.
In section 2.2.3 we concluded that the free volume available to a rod is independent of fugacity. Therefore the complete phase diagram for the needle-sphere mixtures including the fluid-solid transitions can be obtained using first-order perturbation theory.
The coexistence densities for the solid-liquid and the solid-gas
transition are easily calculated from the chemical potentials and the
pressures in eqn.
2.14-2.15.
The resulting phase diagrams for different rod lengths are shown in figure 2.4. The most obvious result is that a stable liquid-gas two-phase region is indeed possible.
If the rods get smaller than 0.3
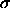the vapor-liquid phase separation becomes metastable. One can imagine that at this point the rods start to fit in the interstitial spaces of the solid phase. This causes the free energy of the solid vapor equilibrium to be lower than that of the liquid vapor equilibrium.
As discussed above the coexistence curves shift to lower fugacities with increasing rod length. The interaction range between the particles becomes larger and the necessary depth of the effective potential to induce phase separation which is governed by the rod fugacity is smaller.
The fluid-solid coexistence region becomes wider at high fugacity. This is a common phenomenon in fluid-solid transitions. If the fugacity increases, the free energy in the fluid decreases more than the free energy of the solid. To compensate this, the equilibrium solid phase has to become denser and the fluid phase more dilute.
section 2.3
subsection 2.3.3 
.
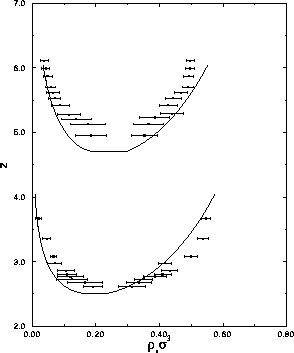
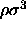The upper curve and points correspond to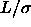 
=2, the lower to
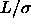=3.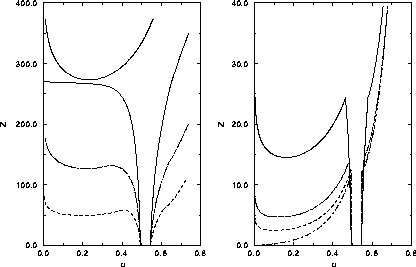 
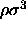. The lines correspond to the phase
boundaries and are obtained by first-order perturbation theory as
given in the text. Left picture: solid line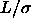 
=0.2, dotted line
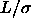=0.3, dashed line 
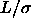=0.5. Right picture: solid line 
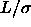=1, dotted
line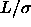 
=2, dashed line 
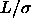=3 and dot dashed line
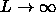. The solid curve in the left picture is the metastable fluid-fluid binodal for 
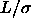=0.2.