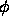of spheres and fugacity z of the needles is given by
section 2.2
subsection 2.2.3
Although the Gibbs-ensemble simulations described above indicate that a fluid-fluid like demixing occurs in the sphere-needle mixture, it is not obvious that this phase equilibrium can indeed be observed in experiments. In particular, the fluid-solid transition might take place before the fluid-fluid two phase region is reached. It is therefore essential to study the stability of the fluid phase with respect to the solid. To locate the freezing transition we must compute the Helmholtz free energy of both the fluid and solid phases. This free energy is best computed by thermodynamic integration, using the hard-sphere system as a reference. The Helmholtz free energy of a sphere-needle mixture at volume-fraction 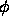of spheres and fugacity z of the needles is given by
where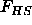 
is the hard sphere reference energy and 
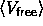the average free volume available to the rods.
This free volume is a function of the fugacity. We performed
simulations to obtain the free volume for a rod in the dense fluid and
the solid phase at different fugacities. For the solid we assumed an
fcc crystal structure which is presumably the most stable solid phase of hard spheres.
Figure 2.2 shows the measured average free volume fraction for one rod as a function of the hard sphere volume fraction for several needle fugacities. The free volume available to the needles is almost independent of the fugacity. The fluid structure is therefore only slightly affected by the addition of needles. Because the free volume is effectively independent of fugacity we can use first order perturbation theory to calculate the free energy at higher fugacities. Therefore eqn. 2.11 reduces to
where 
is the free volume for one rod in the hard sphere reference system.
From this equation the coexistence densities of both the fluid and the solid phase can be obtained by equating the pressure and chemical potentials in both phases.
For the fluid hard sphere equation of state we used the Carnahan-Starling expression [37] whereas the solid hard-sphere equation of state and reference free energy were obtained from simulation data [38,39].
Although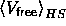 
could be obtained from simulation data, we found that in the fluid phase it could be approximated quite well by scaled particle theory (SPT) [40].
In the solid phase the SPT considerably overestimates the free volume. This is not surprising as the theory was derived for the fluid region. However, as the free volume in the solid is very small anyway, the overestimate will not alter the thermodynamic properties of the mixture unless one considers very high polymer fugacity [10].
section 2.2
subsection 2.2.1
for
infinitely thin rods of length 
=2 as a function of hard
sphere volume fraction 
. Simulation parameters as given in the
text. The main figure gives the free volume in the fluid phase,
whereas in the inset the much smaller free volume of the solid phase
is plotted. The symbols refer to different rod fugacity: 
=2.7, 
=7.4, 
=12.2 and 
=20.1. The solid curve is the scaled particle theory approximation to the free volume for 
=2. Note that the relative difference of the simulated data and the SPT curve is larger in the solid phase.