Next: Infinitely long-ranged attraction Up: Mixtures of spherocylinders Previous: Results
Next: Infinitely long-ranged attraction
Up: Mixtures of spherocylinders
Previous: Results
The existence of a nematic-nematic phase transition in systems of
rods with an attractive potential was already
predicted in the early work of Flory [119] and later by
Khokhlov and Semenov [120]. They estimated that a
nematic-nematic transition can occur for rods with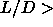 
15, but will
be metastable for smaller elongations.
To investigate the possibility of a polymer-induced N-N transition for suspensions of long rods,
we study the phase behavior of a system of infinitely long ("Onsager") rods.
The details of this type
of simulation were discussed in chapter 5 in the context of hard spherocylinders. If we now wish to include the depletion interaction, we must extend the generalized square-well interaction
discussed in section 6.3 to long rods in the limit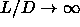 
. As in chapter 5, we assume that the system is either in the dense nematic phase, or in an even more highly ordered phase, such that the rods are almost perfectly aligned. This allows us to use an affine transformation to map the long spherocylinder system onto skewed right cylinders with aspect ratio one.
Note that the same affine transformation will map an Asakura-Oosawa sphere onto a disk.
All the depletion interactions are therefore limited to points on the same xy-plane.
The total depletion potential can be obtained by integrating all in-plane interactions along the two rods.
(i.e. by integrating z in the interval where both cylinders are intersected by the same xy-planes).
where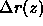 
is the distance between the axes of the two rods
in the xy-plane at height z. Of course, we should take
the effect of the finite length of the rods into account.
As in section 6.3.1, this integral can be given a simple
geometrical interpretation.
| Figure: | Geometrical representation of the
computation of
the polymer induced depletion potential for spherocylinders in the
limit  .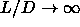
On the left, two interacting scaled spherocylinders are depicted. The
range of the square well is indicated by the dashed spherocylinder.
The fraction of the length
of the right cylinder that is inside this dashed volume, is
proportional for the interaction potential, according to
eqn.
6.6.
Figure b) is a projection along the cylinder axis of one of the scaled
spherocylinders. The dashed circle gives the boundary of the square
well interaction. The thick line-segment is the projection of that
part of the axis of the other
cylinder that is located between the top and bottom surfaces of the
first cylinder. We denote the (unprojected) length of this segment by
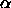 . The fraction of the line segment inside the dashed circle
circle is denoted by 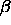 . The value of the integral in
eqn.
6.6 is given by  . |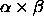
| Figure: | The phase diagram for a system of
infinitely long hard rods,
with an attractive interaction given by eqn.
6.6. The range
of the attraction is 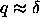 =1. The
diagram is plotted in the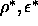 
plane to make comparison with the rod-polymer mixture possible. The
dashed curve is the metastable N-N binodal. |
In figure 6.6 we consider two particles i and j at a
center of mass distance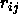 
. The top surface of skewed cylinder
i (j) is shifted with respect to the bottom by an amount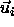 
(
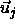). We can deform the coordinate frame such that the
axis of one particle (say i) is along the z-axis. Projecting
cylinder i along the z-axis, we can draw a circle of radius
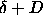around the particles axis, which shows the range of the
square well potential. In the same figure, we project that fraction
of the axis of particle j that is located between the top and bottom
planes of particle i. We denote the length of this segment by
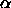. Next, we project this line segment on a plane perpendicular
to the z-axis. The resulting line segment may intersect the circle
that delimits the range of the square well potential. Let us denote by
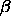, the fraction of the projected line segment that lies within
this circle. The interaction strength of particle i and j is then
given by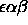 
. Obviously, the maximum interaction
strength,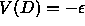 
, is found for two parallel particles at
contact and at equal height.
We performed simulations of the Onsager system for the nematic and smectic
phases with densities between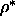 
=0.1 and 
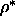=0.7.
The width of the potential well
was chosen to be 
=1, while the well depth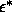 
was
varied between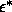 
=0 to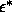 
=2.5.
We measured the average potential energy as a function of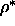 
and
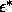and constructed a
free-energy surface for the nematic and smectic phases by thermodynamic
integration, starting from the known equation of state of the
pure Onsager particles (chapter 6.4).
A nematic-nematic
transition shows up as non-convex behavior of the volume
dependence of this free energy. The nematic-smectic transition,
although presumably continuous in the pure Onsager system, becomes
first order upon introducing an attraction.
The calculated phase diagram is shown in figure 6.7.
Clearly, the nematic-nematic separation is (just) metastable with respect to
the nematic-smectic transition.
We expect that the N-N binodal shifts to lower reduced density
and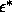 
as the range of attraction becomes larger. For
sufficiently long ranged attractions, there could be a stable N-N
binodal.
To check this, we studied a system with infinitely long-ranged (but
infinitely weak)
attraction. That is, we analyse the ``van der Waals'' limit of the
Onsager system plus attraction.
