


Next: Nematic-Nematic coexistence in Up: Spherocylinders with attraction Previous: Simulation



Next: Nematic-Nematic coexistence in
Up: Spherocylinders with attraction
Previous: Simulation
| Figure: | Simulated phase diagrams for
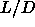 =5
spherocylinders with an attractive generalized square-well potential
(eqn.
6.1). The diagrams are plotted in the =5
spherocylinders with an attractive generalized square-well potential
(eqn.
6.1). The diagrams are plotted in the 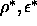 plane to facilitate comparison with the Asakura-Oosawa model of
rod-polymer mixtures.
plane to facilitate comparison with the Asakura-Oosawa model of
rod-polymer mixtures. |
The results of the thermodynamic integration are displayed in
figure 6.5 for different values of 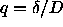 .
The graphs are plotted in the
.
The graphs are plotted in the 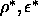 plane instead of the usual
plane instead of the usual 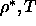 plane because the well depth
plane because the well depth
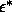 is more directly related to the fugacity of the polymers in
the system. In this way one can compare the phase diagrams with those
of section 6.2. We note, however, that the pair potential that we use
is not completely equivalent to the Asakura-Oosawa interaction. For this reason we focus on the qualitative features of the phase diagram.
For q=1 the range of the potential is equal to the diameter of the
spherocylinder and we see a phase separation between two isotropic
phases ending in a critical point. The isotropic-isotropic phase
separation is similar to the fluid-fluid coexistence in
chapter 2.
The density region where the nematic phase is stable becomes
narrower as
is more directly related to the fugacity of the polymers in
the system. In this way one can compare the phase diagrams with those
of section 6.2. We note, however, that the pair potential that we use
is not completely equivalent to the Asakura-Oosawa interaction. For this reason we focus on the qualitative features of the phase diagram.
For q=1 the range of the potential is equal to the diameter of the
spherocylinder and we see a phase separation between two isotropic
phases ending in a critical point. The isotropic-isotropic phase
separation is similar to the fluid-fluid coexistence in
chapter 2.
The density region where the nematic phase is stable becomes
narrower as  increases and it ends in an isotropic-nematic-smectic triple point at a fugacity of
increases and it ends in an isotropic-nematic-smectic triple point at a fugacity of
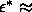 0.23. This is lower than the location of the
0.23. This is lower than the location of the 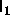 -
-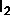 -
-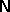 triple
point at
triple
point at 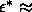 0.34. In contrast, the results of the
perturbation theory in section 6.2 indicate that for q=1 the I-N-SmA
triple point has a higher fugacity than the
0.34. In contrast, the results of the
perturbation theory in section 6.2 indicate that for q=1 the I-N-SmA
triple point has a higher fugacity than the 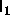 -
-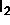 -
-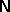 one. Apparently, the attractive pair potential destabilizes the
nematic phase with respect to the smectic phase.
one. Apparently, the attractive pair potential destabilizes the
nematic phase with respect to the smectic phase.
At higher fugacity the smectic phase is expected to become metastable with respect to the
solid. Although we have not included the solid in our simulation, it is likely that the
general picture is similar to that found in section 6.2.
The perturbation theory of section 6.2 predicts that, for
smaller values of q, the isotropic-isotropic transition will shift to higher
fugacity and density and will, eventually be preempted by the isotropic-nematic transition.
Indeed, for q=0.5 we find that the I-I transition has already disappeared.
The I-N and N-SmA transitions widen at higher 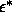 . The
I-N-SmA triple point is located at
. The
I-N-SmA triple point is located at 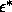 =0.3. For still smaller q, the
picture remains much the same. The I-N and N-SmA transitions
widen at high
=0.3. For still smaller q, the
picture remains much the same. The I-N and N-SmA transitions
widen at high 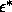 , the triple point moves to higher
, the triple point moves to higher 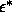 and lower
and lower 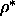 . This last feature was not predicted by the
perturbation theory.
. This last feature was not predicted by the
perturbation theory.
We do not observe a nematic-nematic or
smectic-smectic phase separation. In section 6.2, we argued that
a nematic-nematic or
smectic-smectic transition will, most likely, be preempted by a transition to
a phase with a different symmetry.
However, for large 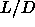 , the range of stability of the nematic phase will become very large.
Under those circumstances, it is likely that a N-N phase-transition
becomes possible
, the range of stability of the nematic phase will become very large.
Under those circumstances, it is likely that a N-N phase-transition
becomes possible


