Next: Overview of demixing Up: Nematic-Nematic coexistence in Previous: Nematic-Nematic coexistence in
Next: Overview of demixing
Up: Nematic-Nematic coexistence in
Previous: Nematic-Nematic coexistence in
Thermodynamic perturbation theory becomes exact in the limit of infinitely
weak, infinitely long attraction [5]. This is the basis of the
success of the van der Waals model. We can use
a similar mean-field theory to
examine the phase behavior of
spherocylinders with an infinitely long-ranged interaction in the limit
.
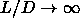The van der Waals free energy
is the sum of the free energy of the hard core reference system and
the change in free
energy due to the attractive interactions.
In the limit of infinitely long-ranged attractions, mean field theory
is exact, and
the perturbation is simply proportional to the density
Here, the parameter a is a measure for
the strength of the attractive interactions or, equivalently, a
measure for the (inverse) temperature. In the polymer-colloid case,
a is a measure for the polymer fugacity.
The phase diagram for the Onsager system with long-ranged attraction
is displayed in
figure 6.8. Clearly there now is a nematic-nematic
transition, which ends
in a critical point at a density of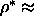 
0.19. We also include the I-N and the N-SmA transition in the
figure, in order to show that the N-N is stable with respect
to these transitions. As before, the N-Sma transition, widens at
large values of a ( higher fugacity). In the Onsager model, the I-N
transition is located
at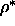 
=0 and is therefore not visible in the figure.
In summary, it is indeed possible to have a stable
nematic-nematic phase separation
in a system of infinitely long hard spherocylinders with attraction,
provided that the interaction is sufficiently long ranged.
If we now consider the van-der-Waals limit for spherocylinders with a
large but finite aspect ratio, the situation changes slightly. We know
(see chapter 5) that the isotropic-nematic transition
moves to higher densities as we move away from the Onsager limit,
while the density of the N-SmA transition is hardly affected. As a
consequence, it is now possible that the isotropic-nematic transition
will interfere with the N-N transition. And this is precisely what
happens: figure 6.9 shows that the N-N phase separation in
the limit of infinitely long-ranged attractions, is preempted by the
I-N transition. The figure suggests that the aspect ratio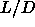 
=40 is
close to the limit where N-N transitions are possible. Only slightly
longer rods would be needed, to recover the N-N binodal.
The perturbation theory calculations indicate that shortening the range of attraction (i.e. decreasing the value of q) will move the critical demixing point to higher densities and will also lead to a reappearance of the N-N transition, until, in its turn, it is preempted by the N-SmA transition at small q values.
This picture corresponds qualitatively to the prediction of Khokhlov
and Semenov[120] that the N-N transition is only possible for
rods longer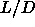 
=15.
The significant difference with our lower limit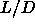 
=40 cannot be
explained by the isotropic attraction, because both theory and simulation
use the same isotropic (exact) mean field potential. Therefore, the
discrepancy must be due to the way the orientation
dependent interactions are treated. In the theory they are
approximated by a simple anisotropic potential, whereas in the
simulations are determined by the (many body) excluded volume of the rods.
We note that, although the depletion interaction between colloids in the limit of infinitely long polymers is well described by the van der Waals model for low polymer density, the model breaks down at higher density because of the many-body character of the depletion interaction. For instance, as we saw in chapter 1, the critical point of the fluid-fluid binodal shifts to zero colloid density in this limit, whereas the van der Waals model predicts a finite density. However, this difference will not qualitatively affect the existence of the nematic-nematic transition in a mixture of elongated spherocylinders and large polymers.
| Figure: | Schematic summary of the regions of in the phase diagram of spherocylinder polymer mixtures, where demixing into two phases with the same symmetry can occur. See text. |
=40 spherocylinder
system with an infinitely long ranged, infinitely weak, attractive
potential. The nematic-nematic binodal is preempted by the
isotropic-nematic transition.