


Next: Simulation Up: Spherocylinders with attraction Previous: Spherocylinders with attraction



Next: Simulation
Up: Spherocylinders with attraction
Previous: Spherocylinders with attraction
In the previous section we used perturbation theory to estimate the
phase behavior of the Asakura-Oosawa model for rod-polymer
mixtures. The crucial assumption in the
perturbation theory is that we can use
the properties of the hard spherocylinder reference fluid to compute
the free-volume fraction 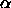 at
finite fugacity. To check if this assumption is justified, we have to
perform simulations of the full Asakura-Oosawa model at finite z.
Although this is certainly feasible for individual state points, such
calculations would become prohibitively expensive if we wish to
compute phase diagrams for different values of q and different
aspect ratios of the rods. The reason is that, in a full (off-lattice)
simulation of the AO model, every polymer has to be
simulated separately. The number of particles needed for such
simulation is quite large, certainly for the small polymers at high
fugacities.
As an example we can estimate the number of polymers in a nematic phase
of spherocylinders of
at
finite fugacity. To check if this assumption is justified, we have to
perform simulations of the full Asakura-Oosawa model at finite z.
Although this is certainly feasible for individual state points, such
calculations would become prohibitively expensive if we wish to
compute phase diagrams for different values of q and different
aspect ratios of the rods. The reason is that, in a full (off-lattice)
simulation of the AO model, every polymer has to be
simulated separately. The number of particles needed for such
simulation is quite large, certainly for the small polymers at high
fugacities.
As an example we can estimate the number of polymers in a nematic phase
of spherocylinders of 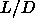 =5 at a density
=5 at a density 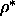 =0.5 in
equilibrium with a reservoir with polymers of diameter
=0.5 in
equilibrium with a reservoir with polymers of diameter 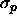 =0.15.
As can be seen in figure 6.2, the polymer fugacity can easily
be equal to
=0.15.
As can be seen in figure 6.2, the polymer fugacity can easily
be equal to 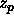 =10. The free volume fraction for this density and
q-value is approximately 0.4.
This corresponds to an equilibrium polymer density in the
nematic phase of
=10. The free volume fraction for this density and
q-value is approximately 0.4.
This corresponds to an equilibrium polymer density in the
nematic phase of 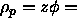 4. As the volume of the
simulation box has to be larger than
4. As the volume of the
simulation box has to be larger than 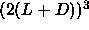 to avoid multiple
overlaps of the spherocylinders,
the minimum number of polymers needed in such is simulation is
to avoid multiple
overlaps of the spherocylinders,
the minimum number of polymers needed in such is simulation is
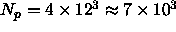 . This is a lower bound, as the
polymers tend to drive the spherocylinders together and
create more space for themselves. Moreover, due to the large particle
concentration, the acceptance probability of moving a spherocylinder in
a sea of polymers is dropping dramatically.
. This is a lower bound, as the
polymers tend to drive the spherocylinders together and
create more space for themselves. Moreover, due to the large particle
concentration, the acceptance probability of moving a spherocylinder in
a sea of polymers is dropping dramatically.
To avoid simulating the full polymer-colloid model, while retaining
the effect of the depletion interaction on the structure of the
colloidal suspension, we constructed a model of hard spherocylinders
with a pairwise additive attractive ``depletion'' potential that
approximates the real potential of mean force W
as introduced in chapter 1.
The most important feature of this potential is that it must be
dependent on relative orientation of the rods. The depletion
attraction is strong (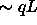 ) when the spherocylinders are
parallel, but much weaker (
) when the spherocylinders are
parallel, but much weaker (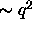 ) for perpendicular rods.
) for perpendicular rods.
The most direct way to compute the depletion pair potential is to calculate the overlap volume between the depletion zones of the two spherocylinders as a function of distance and relative orientation, and multiply this volume by the polymer osmotic pressure. This procedure yields an effective pair potential that can be used in simulations of the phase diagram. In the case of spherical colloids mixed with small polymers, this approach predicts a phase diagram that is in reasonable agreement with the ``exact'' phase diagram [10,6].
| Figure: | Geometrical representation of the
computation of the effective depletion interaction between two
spherocylinders (eqn.
6.1). On the left, the situation for two
perpendicular spherocylinders is depicted. The 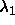 and and
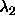 axes denote the distance from the center of mass along a
cylinder axis. The circle indicates the axes denote the distance from the center of mass along a
cylinder axis. The circle indicates the 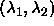 points for which the distance equals
points for which the distance equals 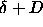 . Inside this circle
the distance is smaller than . Inside this circle
the distance is smaller than 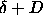 . As the integral
in eqn.
6.1 is bounded by the length of the spherocylinders,
the total interaction is proportional to the cross section of the . As the integral
in eqn.
6.1 is bounded by the length of the spherocylinders,
the total interaction is proportional to the cross section of the 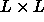 square and the ellipse.
On the right, the angle between the spherocylinder is less than 90
degrees. The circle therefore changes into an ellipse, with its major
axes along the lines square and the ellipse.
On the right, the angle between the spherocylinder is less than 90
degrees. The circle therefore changes into an ellipse, with its major
axes along the lines 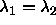 and and 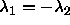 . The interaction is still proportional to the area bounded
by the ellipse and the condition . The interaction is still proportional to the area bounded
by the ellipse and the condition 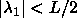 and and 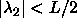 . . |
Although the depletion pair-potential for spherocylinders could be
computed in the same way, the resulting function would not be
cheap to compute during a simulation. As the computation of the pair
potential is the most time-consuming part of the program, it is
useful to devise an effective pair potential that resembles the
depletion interaction, but is computationally cheap.
To this end, we assume that the spherocylinder can be considered as a
continuous distribution of (overlapping) spheres of diameter D, with
their centers distributed uniformly on a line segment of length
L. The individual spheres interact through a square-well potential.
The total pair potential of the two spherocylinders is then a sum (or
actually, an integral) of
all the individual contributions, and is expressed as:
Here 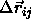 denotes the relative position of the centers of mass of
the two hard spherocylinders i and j, with
orientations specified by the unit vectors
denotes the relative position of the centers of mass of
the two hard spherocylinders i and j, with
orientations specified by the unit vectors 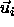 and
and 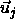 ,
respectively. The range of depletion interaction
(
,
respectively. The range of depletion interaction
( ) is a measure for
the polymer diameter
) is a measure for
the polymer diameter 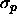 . The well depth
. The well depth  can be
interpreted as a measure for the polymer concentration. The Heaviside
step-function
can be
interpreted as a measure for the polymer concentration. The Heaviside
step-function 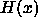 is defined in the
usual manner:
is defined in the
usual manner:

The evaluation of the integral in eqn.
6.1 can be reduced to
a simple geometrical problem. First, consider the interaction between
two infinitely long cylinders. If the cylinders are mutually
perpendicular, the integral will reduce to the calculation of the
surface of a circle with radius 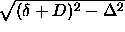 ,
where
,
where 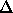 is the minimum distance between the lines that run
through the cylinder axes. As the angle between the cylinders becomes
smaller, this circle changes into an ellipse by scaling one of the
ellipse axes by
is the minimum distance between the lines that run
through the cylinder axes. As the angle between the cylinders becomes
smaller, this circle changes into an ellipse by scaling one of the
ellipse axes by 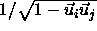 . The integral diverges for
parallel, infinite cylinders, because every point along the cylinder
gives a finite contribution. However, the integral in
eqn.
6.1 is bounded by the finite length of the
spherocylinders. This is translated in the geometrical picture as
cuts through the ellipse, as shown in figure 6.3.
If we multiply the area enclosed by the ellipse and/or the cuts of the
. The integral diverges for
parallel, infinite cylinders, because every point along the cylinder
gives a finite contribution. However, the integral in
eqn.
6.1 is bounded by the finite length of the
spherocylinders. This is translated in the geometrical picture as
cuts through the ellipse, as shown in figure 6.3.
If we multiply the area enclosed by the ellipse and/or the cuts of the
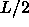 bounds by the well depth
bounds by the well depth  we obtain the total
interaction potential.
we obtain the total
interaction potential.
A quantity of particular interest is the maximum interaction between two spherocylinders. The interaction between two particles is largest when they are oriented parallel with their centers of mass at the minimum distance (D).
In figure 6.4 we show the behavior of this pair potential for a few relative orientations and distances of the two spherocylinders.


