SIMULATION

We performed NVT Monte Carlo simulation on a system of 480 spherocylinders with 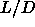=5 interacting through the generalized square-well potential described in the previous section, for 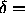0.1, 0.3, 0.5 and 1.0. The density ranged from 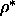=0.1 in the isotropic phase to 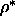=0.66 in the smectic phase. The reduced well depth 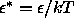is a measure for the polymer concentration. In our simulations, it ranged from 0--2. Configurations of the system at high densities were generated by slowly expanding a perfectly aligned, close packed smectic structure. Care was taken to avoid that the system became stuck in glassy configurations, a problem that was particularly severe at low temperatures (large 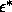). We measured the potential energy as a function of 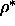and 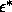and fitted it to a polynomial of the form

The free energy of the system could be obtained via thermodynamic integration (see chapter 3)

where 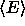is the average potential energy measured during the Monte Carlo simulations and 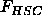denotes the free energy of the hard spherocylinder reference system. This free energy can be obtained by integration along the equation of state in the different phases, where the reference free energies were taken from the results of section 5.4 of chapter 5.

At large 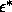(low T), the Helmholtz free energy 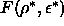may exhibit an inflection point, signalling the occurrence of a first-order phase transition within a single phase (e.g isotropic-isotropic). Alternatively, the increased attraction may shift the phase coexistence boundaries of the I-N, N-SmA or SmA-S transitions. In either case, we can estimate the density of the coexisting phases by using a double tangent construction.