PERTURBATION THEORY

The thermodynamic perturbation theory of ref. [113] requires as input the equation of state of the hard core reference system (in this case, the hard spherocylinder fluid) and the free-volume fraction 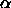. The previous chapter (chapter 5) contains the necessary information about the equation of state of a pure hard spherocylinder fluid. In addition, we measured the free volume function 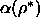as a function of density by use of the Widom insertion technique [36]. The advantage of the perturbation approach is that there is no need to simulate the polymers explicitly: it is sufficient to just measure the free volume available for a polymer in a pure hard spherocylinder system. We should stress that there is a slight difference in the philosophy underlying the present (numerical) implementation of perturbation theory and the scaled-particle theory approach of ref. [113]. Stroobants and Lekkerkerker minimize the free energy of the polymer-colloid mixture with respect to the orientational distribution function of the rods. Hence, in their case, the orientational distribution function of the mixture is not equal to the distribution function of the pure reference system at the same density. In our simulations, we do not attempt to vary the orientational distribution function independently of density (as this would involve performing many simulations of a hard spherocylinder fluid in a magnetic field).
In the Widom method, we attempt to insert polymers (represented by hard spheres) at random positions in the simulation box. The fraction of insertions that does not result in an overlap corresponds to the free volume fraction. In practice, we measure the distance r to the nearest surface of a spherocylinder. A polymer with a radius larger than r will overlap with the spherocylinder, while a smaller polymer will fit. We made a histogram of the insertion probability, and hence the free volume fraction 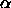, as a function of 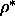and q. We fitted this free volume data to a polynomial in 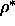and q and used equations 1.19 and 1.20 in combination with the simulation results for 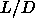=5 (chapter 5) to calculate the two-phase coexistence curves. The resulting phase diagrams in the 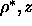plane are presented in figure 6.2 for q= 0.15, 0.25, 0.50, 0.65, 0.75 and 1.0. These figures show the thermodynamically stable regions of the isotropic, nematic, smectic A and solid phase denoted respectively by I,N,SmA and S respectively. The phases are separated from each other by first-order coexistence regions indicated by a grey area. Two coexisting phases will have equal z, because z is the fugacity of the polymer reservoir that is in equilibrium with both phases. In figure 6.2 a) the phase diagram for q=1.00 is depicted. The isotropic fluid phase contains the familiar binodal curve ending in a critical point. This binodal is very similar to the ones we obtained in chapter 2 and 3. At a fugacity higher than 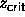=0.95 a phase separation occurs between a vapor phase with a low density of spherocylinders, and a high density liquid phase. Upon increasing the fugacity of the polymers, the liquid becomes metastable with respect to the nematic phase and we find gas-nematic coexistence. At still higher fugacity the nematic phase also disappears and there is a two phase gas-smectic coexistence region. Eventually, at z=2.5 the gas-smectic is preempted by the crystallization transition. The important difference with the theoretical predictions of figure 6.2 is that the scaled-particle theory of ref. [113] does not consider the smectic and solid phases. We find that the densities of the coexisting phases at the I-N, N-SmA and the SmA-S transitions, hardly change with the polymer fugacity.

In figure 6.2 b) we consider the situation for a smaller polymer radius of q=0.75. As expected, the shorter interaction range results in a shift of the critical point of the I-I demixing transition to higher densities. Moreover, the transition occurs at higher polymer fugacity. We note that the I-N coexistence density gap widens (slightly) at higher polymer fugacity. The density region where the nematic phase is stable does, therefore, decrease at these high polymer fugacity. The I-I-N triple point occurs at somewhat higher fugacity. The I-N-SmA and I-SmA-S triple points are hardly affected.

When we decrease the range of interaction to q=0.65, the critical point of the I-I demixing curve disappears. The I-I binodal has moved to higher fugacity where the phase transition is preempted by the (successively) I-N, I-SmA and I-S transitions. The I-N-SmA and I-SmA-S triple points still occur at roughly the same polymer fugacity, although close to the triple points, all three first order phase coexistence regions widen somewhat.

For q=0.50 the widening of the N-SmA transition becomes very pronounced for z>1.5. The I-N-SmA triple point increases in fugacity faster than the N-SmA-S triple point. This shift in the relative location of triple points continues and for q=0.25 the N-SmA-S occurs at lower z than the I-N-S triple point. The interaction range is now small enough to affect the SmA-S transition. The shape of the coexistence curve in the solid phase is typical of a system approaching an isostructural solid-solid transition. However, the interaction ranges is still too large to induce such a phase separation inside the solid phase. As we saw in chapter 3, in the case of spherical colloids this transition occurs only if the interaction range is less than 0.07. The last plot of figure 6.2 shows the phase diagram for q=0.15. The SmA-S transition has become even wider, and the I-N-S and the N-SmA-S triple points both move to higher z-values, but their relative position is hardly affected.

Summarizing, the global picture that follows from this perturbation theory calculation is as follows. For large polymers we have an isotropic fluid-fluid phase separation ending in a critical point which shifts to larger z and 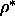and is preempted when the radius becomes smaller then q=0.6. The I-N-SmA and I-SmA-S triple points occur at z=2.2 and 2.5 respectively and are not very sensitive to the polymer size for q>0.6. For lower q both triple points move to higher z, but the I-N-SmA overtakes the I-SmA-S triple point. For q<0.45 the situation changes and we have and I-N-S and a N-SmA-S triple point. For the low q values the I-N, N-SmA and SmA-S coexistence regions fan out for high z. We find no evidence for an N-N transition, as predicted by the SPT approach of ref. [113]. In particular, for q=0.1 the scaled-particle theory predicts a N-N critical point at 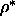=0.6. However, the present simulations suggest that, at that density, the nematic phase is no longer stable with respect to the smectic. The perturbation theory that we use becomes less accurate at high z, because it neglects any structural changes induced by the polymer. Still, this limitation is unlikely to affect our conclusion that a polymer-induced N-N phase separation will not occur for rods with an aspect ratio 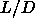=5. After all, the density range over which the nematic phase is stable, is quite limited: there is hardly space for an N-N binodal. We therefore expect a nematic-nematic phase separation to take place for larger elongation of the spherocylinder, where the nematic phase extends over a much wider density range.

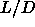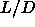For the same reason, it is unlikely that there is a smectic to smectic transition for =5. Moreover, increasing the aspect ratio of the rods will do little to facilitate the occurrence of a smectic-smectic transition, as the density range where the smectic phase is stable hardly changes with . It is tempting to speculate that polydispersity of the rods may change these conclusions: polydispersity in the length of the rods enhances the nematic stability, thus making a N-N separation more likely. In contrast, polydispersity in the diameter of the spherocylinders widens the smectic range [118]: this may favor the occurrence of a demixing transition in the smectic phase.