OVERVIEW OF DEMIXING TRANSITIONS

On basis of the available results, we can give a rough sketch of the expected regions where demixing transitions should occur in the 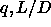plane. In figure 6.10 we have combined our present knowledge about the stability regions of the phase separations in the different phases as a function of the polymer interaction range q and the colloid aspect ratio 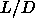. The curves give a rough indication of the regions in the 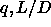plane where the depletion interaction induces a binodal in any one of the phases. The I-I critical point starts to appear for hard spheres around q=0.3. For rods with an aspect ratio 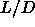=5, the minimum interaction range needed to induce an I-I phase transition, has increased to 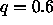and it probably increases steeply with increasing aspect ratio. In fact, beyond a certain aspect ratio (less than 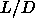=40), stable I-I transition is not even possible in the limit 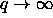. The nematic-nematic transition first appears for systems with an aspect ratio that is large enough to support a nematic phase over a reasonable density range. For finite 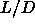values, the region where a N-N transition is possible is bounded on both the low and high q side. The high-q boundary rises steeply with increasing 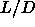, and for large 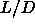, the region where an N-N transition can occur is only bounded for low q. In our simulations, we have not observed a SmA-SmA phase-separation, but there is no a-priori reason to exclude it either. However, as the range of stability of the smectic phase is never very large, we expect the SmA-SmA transition, if it occurs at all, be confined to a narrow ``window'' in the 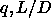plane. A possible location for this window has been sketched in figure 6.10. For very short-ranged attractions (low values of q), we expect to observe an isostructural solid-solid phase transition separation over the entire 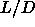range. This solid-solid transition was discussed in chapter 3 for the case of hard spheres. For spherocylinders, we expect to see a solid-solid transition in the plastic phase for small 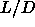(say, 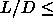0.3). For larger 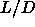values it is possible to have a solid-solid transition between two ordered solid phases (ABC-stacking). 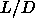Finally, for large values (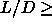10) the solid-solid phase separation takes place between two AAA structures. For hard spheres, the S-S transition in two and three dimensions appears at approximately the same range of the attractive interaction. If we take the point of view that a solid of long spherocylinders resembles a two-dimensional crystal, then it seems reasonable to surmise that the range of q-values for which the solid-solid transition is possible, depends only little on . 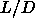It should, however, be stressed that the analogy between a solid of almost very long, well aligned spherocylinders in the AAA-phase, and a two-dimensional crystal of disks, is not perfect, because the orientational entropy of the rods can never be neglected. There are gaps between the three different regions of solid-solid transitions. In those gaps, the effect of the depletion interaction is to widen the density gap between two coexisting solid phases of different symmetry. Finally, it is tempting to speculate that the effect of the depletion interaction on the phase behavior of the AAA-stacked solid, may be even more complex. In a two-dimensional system, the solid-solid critical point induces a hexatic pocket in the phase diagram [50]. Possibly, the solid-solid transition in the AAA-stacked phase favors the formation of a liquid-crystalline hexatic-B phase.