


Next: Perturbation theory Up: Mixtures of spherocylinders Previous: Mixtures of spherocylinders



Next: Perturbation theory
Up: Mixtures of spherocylinders
Previous: Mixtures of spherocylinders
| Figure: | Phase diagrams of hard spherocylinders
with aspect ratio 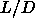 =5,
plus non-adsorbing polymer, as predicted by the scaled particle theory
of Lekkerkerker and Stroobants [113]. In this theory, the
polymers are modeled as inter-penetrable hard sphere, in the spirit of
the Asakura-Oosawa model. The ratio of the diameter of the polymer spheres
to the diameter of the spherocylinders is denoted by q.
The theory of ref. [113] does not consider the smectic and
solid phases. =5,
plus non-adsorbing polymer, as predicted by the scaled particle theory
of Lekkerkerker and Stroobants [113]. In this theory, the
polymers are modeled as inter-penetrable hard sphere, in the spirit of
the Asakura-Oosawa model. The ratio of the diameter of the polymer spheres
to the diameter of the spherocylinders is denoted by q.
The theory of ref. [113] does not consider the smectic and
solid phases. |
For over half a century, experimentalists have known that the
isolation and purification of rodlike viruses, such as the
tobacco-mosaic virus (TMV), can be facilitated by addition of
non-adsorbing polymers [114]. As purification of the virus was the
central theme of these experiments, little attention was paid to the
underlying physics of such mixtures of polymers and rodlike
colloids. Yet, TMV dispersions provide excellent model systems to
study colloidal liquid crystalline phases [100].
However, a limitation of the TMV system is that the length of the
particle cannot be varied at will. Less seriously, the rod-rod
interaction is predominantly electrostatic. This complicates a direct
comparison to theories for hard rod suspensions. In recent years,
much effort has been invested in the development of reliable
techniques to synthesize sterically stabilized rodlike colloidal
boehmite needles [115]. Dispersions of such particles could
serve as a model system for rodlike colloids, much in the same way as
dispersions of spherical latex and silica particles act as
proto-typical experimental realizations of hard-sphere fluids. The
boehmite rods have the added advantage that the length-to-width ratio
can be varied. Thus far, these boehmite suspensions are still fairly
polydisperse, but the situation is likely to improve as more
sophisticated colloid synthesis techniques are developed. Buitenhuis
et al.[116] conducted experiments on a mixture of
polystyrene and boehmite rods with an aspect ratio 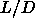 =6.4,
sterically stabilized with poly-isobutene [117] and dispersed
in an organic solvent. For a polymer radius of gyration which was
about 80% of the rod diameter they observed phase separation into two
isotropic phases at sufficiently high polymer concentration.
=6.4,
sterically stabilized with poly-isobutene [117] and dispersed
in an organic solvent. For a polymer radius of gyration which was
about 80% of the rod diameter they observed phase separation into two
isotropic phases at sufficiently high polymer concentration.
The phase behavior of rod-polymer mixtures has been studied
theoretically in the context of the Asakura-Oosawa (AO) model. As
explained in chapter 1, the AO model describes the
polymer as a sphere that has a hard core interaction with the rods,
but is completely penetrable to other polymer spheres. Lekkerkerker
and Stroobants [113] have used the formalism described in
chapter 1 in combination with scaled particle theory to
predict the phase diagram for mixtures of spherocylinders with an
aspect ratio 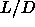 =5 and polymers with q= 1.0, 0.8, 0.5 and 0.1, where
q is defined as the ratio of the (hard sphere) polymer diameter and
the spherocylinder hard core diameter (
=5 and polymers with q= 1.0, 0.8, 0.5 and 0.1, where
q is defined as the ratio of the (hard sphere) polymer diameter and
the spherocylinder hard core diameter (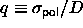 ). Scaled particle theory provides the equation of state for pure
hard spherocylinder systems and the free volume fraction
). Scaled particle theory provides the equation of state for pure
hard spherocylinder systems and the free volume fraction
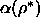 required in the perturbation theory. The free energy
of the nematic phase depends functionally on the orientational
distribution function. The equilibrium orientational distribution
minimizes the free energy. Figure 6.1 shows the results
of the calculations of Lekkerkerker and Stroobants in the
required in the perturbation theory. The free energy
of the nematic phase depends functionally on the orientational
distribution function. The equilibrium orientational distribution
minimizes the free energy. Figure 6.1 shows the results
of the calculations of Lekkerkerker and Stroobants in the 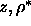 plane. Here z, the polymer fugacity of the reservoir is related to
the reservoir polymer number density
plane. Here z, the polymer fugacity of the reservoir is related to
the reservoir polymer number density 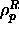 by
by 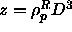 .
As can be seen from the figure, the theory predicts that for
long polymers (
.
As can be seen from the figure, the theory predicts that for
long polymers (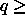 0.8), demixing will occur in the isotropic
phase: this corresponds roughly to the results of the experiments on
boehmite rods, mentioned above [116]. The critical point
of the binodal in figure 6.1 shifts to higher density as
q is lowered. For shorter polymers, this I-I transition disappears.
For instance, for q=0.5, the I-I binodal is metastable with respect
to the I-N transition. And for short polymers (
0.8), demixing will occur in the isotropic
phase: this corresponds roughly to the results of the experiments on
boehmite rods, mentioned above [116]. The critical point
of the binodal in figure 6.1 shifts to higher density as
q is lowered. For shorter polymers, this I-I transition disappears.
For instance, for q=0.5, the I-I binodal is metastable with respect
to the I-N transition. And for short polymers (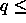 0.1) a
demixing transition is found in the nematic phase. It should be
stressed that the theoretical prediction of the existence of a
nematic-nematic phase separation should be treated with some caution:
in the SPT approach of ref. [113], the smectic-A and solid
phases are not considered, because the approximations that are used to
compute the free-volume fraction
0.1) a
demixing transition is found in the nematic phase. It should be
stressed that the theoretical prediction of the existence of a
nematic-nematic phase separation should be treated with some caution:
in the SPT approach of ref. [113], the smectic-A and solid
phases are not considered, because the approximations that are used to
compute the free-volume fraction 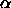 by scaled-particle theory,
are expected to break down in translationally ordered phases.
However, as Lekkerkerker and Stroobants already noted, it is unlikely that the neglect of the smectic A and the
solid phase is justified. There might, for instance, be a
nematic-smectic (or smectic-smectic) phase transition, preempting the
nematic-nematic transition. Even a solid-solid phase transition, as
was discussed in chapter 3 belongs to the
possibilities. In this chapter we will therefore also consider the
influence of polymer addition on the location of the N-SmA and the
SmA-S transition.
by scaled-particle theory,
are expected to break down in translationally ordered phases.
However, as Lekkerkerker and Stroobants already noted, it is unlikely that the neglect of the smectic A and the
solid phase is justified. There might, for instance, be a
nematic-smectic (or smectic-smectic) phase transition, preempting the
nematic-nematic transition. Even a solid-solid phase transition, as
was discussed in chapter 3 belongs to the
possibilities. In this chapter we will therefore also consider the
influence of polymer addition on the location of the N-SmA and the
SmA-S transition.
In the following section we use the results of numerical simulations
on hard spherocylinders with aspect ratio 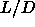 =5, to compute the
free-volume fraction that plays a crucial role in the thermodynamic
perturbation theory as applied to the Asakura-Oosawa model. Using
this perturbation theory, we arrive at a prediction of the phase
diagram of the polymer-colloid mixture. It would be natural to
compare the theoretical predictions with a direct simulation of the
full AO model, at finite polymer fugacity z. However, such
simulations would be computational quite expensive. In section
6.3, we therefore explore an alternative approach: we
replace the polymer-induced depletion force by an angle dependent
attractive pair potential. In section 6.4 we study
the possibility of nematic-nematic phase transitions in the limit of
large
=5, to compute the
free-volume fraction that plays a crucial role in the thermodynamic
perturbation theory as applied to the Asakura-Oosawa model. Using
this perturbation theory, we arrive at a prediction of the phase
diagram of the polymer-colloid mixture. It would be natural to
compare the theoretical predictions with a direct simulation of the
full AO model, at finite polymer fugacity z. However, such
simulations would be computational quite expensive. In section
6.3, we therefore explore an alternative approach: we
replace the polymer-induced depletion force by an angle dependent
attractive pair potential. In section 6.4 we study
the possibility of nematic-nematic phase transitions in the limit of
large 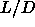 .
.


