section 4.3
Evaluation of the hard sphere fluid-solid coexistence line as a function of polydispersity can be done by application of the Gibbs-Duhem integration method recently developed by Kofke [84]. In this method two phases are simulated simultaneously at the same state conditions. The technique allows a series of simulations to trace a line of coexistence in the plane of two state variables; for the purpose of describing the method let us say that these variables are the temperature and pressure, respectively. Chemical potential equality between the phases is ensured by starting the process with two known equilibrium phases, and subsequently applying thermodynamic integration to select the appropriate pressure while the temperature is varied from one simulation to the next in the series. The integration path may be derived from the Gibbs-Duhem equation
where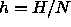 
and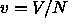 
are the molar enthalpy and volume,
respectively. For two coexisting phases to remain in equilibrium when
the temperature is changed, the pressure must vary in a way that
maintains chemical potential equality between them. The required
change can be derived from eqn.
4.6
where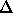 
indicates a difference between the two phases. Eqn
4.7 is known as the Clapeyron equation. It is a simple first
order differential equation which can be integrated using a
predictor-corrector scheme. The 'initial condition' is a known point
at the coexistence line in the T,P plane. By simulating the two
coexisting phases simultaneously at the equilibrium pressure and
evaluating the right hand side of eqn.
4.7, one can predict
the pressure at another temperature not far away. Simulation at this
P and T yields new values of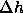 
and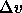 
, which can
be used to correct the predicted pressure while the simulation
continues to proceed. The process is then repeated to get the next
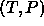coexistence state point. Details of the method may be found
elsewhere [84,88].
In the case of polydisperse hard spheres we do not need the
temperature as an independent variable, but instead we need a measure
for the polydispersity. An obvious choice is 
, as it occurs in
the fundamental equation 4.4. The Gibbs-Duhem equation for
polydisperse mixtures can be derived by combining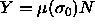 
with eqn.
4.2
Using the same procedure as for the derivation of eqn. 4.4 we obtain
To ensure phase equilibrium,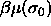 
and the chemical
potential difference function given in eqn.
4.3 must be
the same in the two phases. The latter requirement is fulfilled simply
by using the same 
(and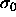 
) in both phases. The first
requirement results in a Clapeyron type of equation which can be
derived from eqn.
4.9 by equating the right-hand side for
both phases and applying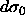 
=0 and 
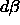=0.
We can integrate in the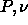 
plane by measuring the second moment
of the composition distribution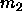 
and the molar volume v in both
phases and applying the predictor-corrector scheme described above.
section 4.3
