chapter 4
 section 4.4
section 4.4
The starting point we use for the Gibbs-Duhem integration is the well
known freezing point of monodisperse hard spheres [56,39]. However, the
initial slope at  =0 given by eqn.
4.10 is not known
here. Moreover, it cannot be calculated directly in a simulation
because both
=0 given by eqn.
4.10 is not known
here. Moreover, it cannot be calculated directly in a simulation
because both 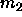 and
and  are equal to zero in the monodisperse
limit, although the ratio
are equal to zero in the monodisperse
limit, although the ratio 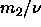 is expected to be finite.
is expected to be finite.
The second moment 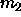 can be calculated if the composition
can be calculated if the composition
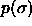 is known. The composition in turn is related to the
chemical potential by
is known. The composition in turn is related to the
chemical potential by

where 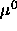 is a collection of terms taken as independent of
is a collection of terms taken as independent of
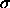 , and
, and 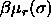 is the residual chemical
potential. With eqn.
4.3, the chemical potential
difference function can now be written as
is the residual chemical
potential. With eqn.
4.3, the chemical potential
difference function can now be written as
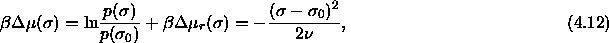
or,
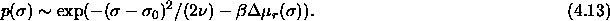
Here, 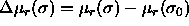 is the
difference in residual chemical potential between a particle with
diameter
is the
difference in residual chemical potential between a particle with
diameter 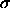 and a particle of the reference component. This
difference can be measured in a simulation of a pure
and a particle of the reference component. This
difference can be measured in a simulation of a pure 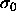 substance by performing `test enlargements', in which a randomly
chosen particle is enlarged from diameter
substance by performing `test enlargements', in which a randomly
chosen particle is enlarged from diameter 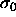 to a random
diameter
to a random
diameter 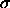 . One tabulates the frequency with which such moves
result in no overlap, although the moves themselves are never
accepted. This overlap probability yields the residual chemical
potential according to
. One tabulates the frequency with which such moves
result in no overlap, although the moves themselves are never
accepted. This overlap probability yields the residual chemical
potential according to
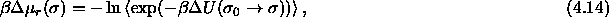
where the brackets indicate the ensemble average; 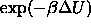 is zero
or unity, respectively, corresponding to the absence or presence of
overlap. This `ghost-growing' procedure is very similar to the Widom 'ghost' particle
insertion technique [36]. In practice, we tabulate the distance
from a randomly selected particle to its nearest neighbor; this
histogram of nearest distances is then easily converted into the
overlap histogram just described.
is zero
or unity, respectively, corresponding to the absence or presence of
overlap. This `ghost-growing' procedure is very similar to the Widom 'ghost' particle
insertion technique [36]. In practice, we tabulate the distance
from a randomly selected particle to its nearest neighbor; this
histogram of nearest distances is then easily converted into the
overlap histogram just described.
For small values of 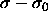 the measured residual chemical
potential might be approximated by a quadratic function
the measured residual chemical
potential might be approximated by a quadratic function

Substituting this in eqn.
4.13 results for the composition
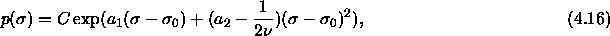
where C is independent of 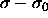 . Because
. Because 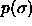 is a Gaussian
function, the desired second moment of the composition
is a Gaussian
function, the desired second moment of the composition 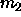 can be
analytically obtained
can be
analytically obtained
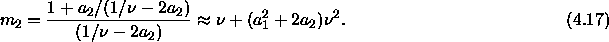
The latter approximation is correct to second order in  . The
initial slope can now be written as
. The
initial slope can now be written as
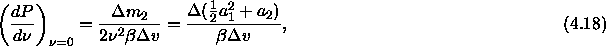
where 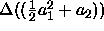 is the difference between
the coefficient expressions evaluated in both phases. In sum, we
measure the residual chemical potential in a simulation of a pure hard
sphere system using eqn.
4.14, we fit it to a quadratic
function for small
is the difference between
the coefficient expressions evaluated in both phases. In sum, we
measure the residual chemical potential in a simulation of a pure hard
sphere system using eqn.
4.14, we fit it to a quadratic
function for small 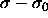 and use the coefficients in eqn.
4.18 to obtain the initial slope for the Gibbs-Duhem
integration.
and use the coefficients in eqn.
4.18 to obtain the initial slope for the Gibbs-Duhem
integration.
chapter 4
 section 4.4
section 4.4
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
 =0 given by eqn.
4.10 is not known
here. Moreover, it cannot be calculated directly in a simulation
because both
=0 given by eqn.
4.10 is not known
here. Moreover, it cannot be calculated directly in a simulation
because both 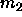 and
and  are equal to zero in the monodisperse
limit, although the ratio
are equal to zero in the monodisperse
limit, although the ratio 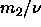 is expected to be finite.
is expected to be finite.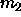 can be calculated if the composition
can be calculated if the composition
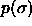 is known. The composition in turn is related to the
chemical potential by
is known. The composition in turn is related to the
chemical potential by

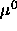 is a collection of terms taken as independent of
is a collection of terms taken as independent of
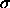 , and
, and 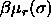 is the residual chemical
potential. With eqn.
is the residual chemical
potential. With eqn.
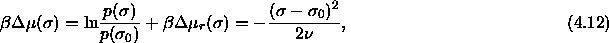
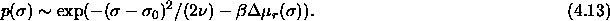
 is the
difference in residual chemical potential between a particle with
diameter
is the
difference in residual chemical potential between a particle with
diameter  and a particle of the reference component. This
difference can be measured in a simulation of a pure
and a particle of the reference component. This
difference can be measured in a simulation of a pure 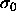 substance by performing `test enlargements', in which a randomly
chosen particle is enlarged from diameter
substance by performing `test enlargements', in which a randomly
chosen particle is enlarged from diameter 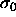 to a random
diameter
to a random
diameter 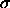 . One tabulates the frequency with which such moves
result in no overlap, although the moves themselves are never
accepted. This overlap probability yields the residual chemical
potential according to
. One tabulates the frequency with which such moves
result in no overlap, although the moves themselves are never
accepted. This overlap probability yields the residual chemical
potential according to
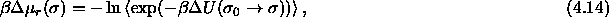
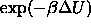 is zero
or unity, respectively, corresponding to the absence or presence of
overlap. This `ghost-growing' procedure is very similar to the Widom 'ghost' particle
insertion technique [
is zero
or unity, respectively, corresponding to the absence or presence of
overlap. This `ghost-growing' procedure is very similar to the Widom 'ghost' particle
insertion technique [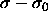 the measured residual chemical
potential might be approximated by a quadratic function
the measured residual chemical
potential might be approximated by a quadratic function

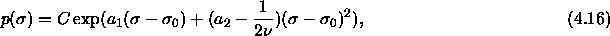
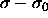 . Because
. Because 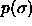 is a Gaussian
function, the desired second moment of the composition
is a Gaussian
function, the desired second moment of the composition 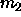 can be
analytically obtained
can be
analytically obtained
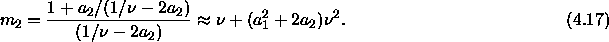
 . The
initial slope can now be written as
. The
initial slope can now be written as
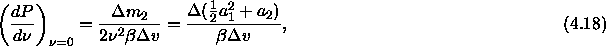
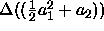 is the difference between
the coefficient expressions evaluated in both phases. In sum, we
measure the residual chemical potential in a simulation of a pure hard
sphere system using eqn.
is the difference between
the coefficient expressions evaluated in both phases. In sum, we
measure the residual chemical potential in a simulation of a pure hard
sphere system using eqn.
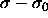 and use the coefficients in eqn.
and use the coefficients in eqn.