chapter 4
 section 4.2
section 4.2
The most straightforward approximation to a continuous mixture is
based in the canonical ensemble and thus takes a finite sample from a
distribution of diameters 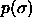 . However, this approach is
sensitive to finite size effects and, moreover, it is not practical
when phase equilibria are considered as it is difficult to ensure
chemical potential equilibration of each component. A better choice
is a grand canonical simulation in which particles of different
species are inserted and removed according to the configurational
energy and the imposed chemical potential of that component. In
this way a truly continuous distribution can be realized and phase
equilibrium can be more easily treated. However, at the high
densities of the liquid-solid equilibrium the insertion probability in
both phases is too low to obtain reasonable statistics; further, the
need to maintain the crystal structure in the solid makes insertions
especially problematic.
. However, this approach is
sensitive to finite size effects and, moreover, it is not practical
when phase equilibria are considered as it is difficult to ensure
chemical potential equilibration of each component. A better choice
is a grand canonical simulation in which particles of different
species are inserted and removed according to the configurational
energy and the imposed chemical potential of that component. In
this way a truly continuous distribution can be realized and phase
equilibrium can be more easily treated. However, at the high
densities of the liquid-solid equilibrium the insertion probability in
both phases is too low to obtain reasonable statistics; further, the
need to maintain the crystal structure in the solid makes insertions
especially problematic.
The semigrand ensemble provides an alternative representation that
combines the best features of the canonical and grand canonical
ensembles for the study of continuous mixtures [85,86].
A simulation in this
ensemble has the total number of particles fixed, but the species
identity of each particle is allowed to change, giving rise to a truly
continuous distribution. Although the chemical potentials are imposed
in a way similar to the grand-canonical ensemble, insertion of
particles is avoided, so the method is suitable for high densities and
crystalline phases.
We consider a system of N hard spheres with diameters 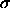 distributed according to
distributed according to 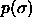 . The isobaric semigrand
canonical free energy Y is defined by a Legendre transform of the
Gibbs free energy G. In the polydisperse limit,
. The isobaric semigrand
canonical free energy Y is defined by a Legendre transform of the
Gibbs free energy G. In the polydisperse limit,
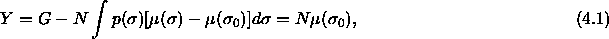
or, in differential form,

Here, 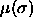 is the chemical potential as a function of
is the chemical potential as a function of
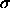 , and
, and 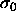 is the diameter of an arbitrarily chosen
reference component. Also, H is the enthalpy,
is the diameter of an arbitrarily chosen
reference component. Also, H is the enthalpy, 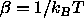 is the
reciprocal temperature, P is the pressure and V the volume of the
system. The isobaric semigrand canonical potential Y is a function of the
independent variables T,P and N and it is a functional of the
chemical potential difference function
is the
reciprocal temperature, P is the pressure and V the volume of the
system. The isobaric semigrand canonical potential Y is a function of the
independent variables T,P and N and it is a functional of the
chemical potential difference function 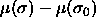 . In a simulation these independent variables must be
fixed while the thermodynamic conjugates
. In a simulation these independent variables must be
fixed while the thermodynamic conjugates 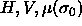 and
and 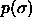 are allowed to fluctuate. This implies that the
composition
are allowed to fluctuate. This implies that the
composition 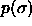 can be known only after the simulation has
been performed. Because the total number of particles is fixed the
chemical potential of the reference
can be known only after the simulation has
been performed. Because the total number of particles is fixed the
chemical potential of the reference 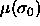 has still to be
computed. Once it is determined, the entire chemical potential
distribution is known. The method is therefore well suited for phase
equilibrium in continuous mixtures: for a given temperature and
distribution in chemical potential differences one needs match only
the values of the pressure and the reference chemical potential in
both phases. This is far simpler than matching the entire distribution
has still to be
computed. Once it is determined, the entire chemical potential
distribution is known. The method is therefore well suited for phase
equilibrium in continuous mixtures: for a given temperature and
distribution in chemical potential differences one needs match only
the values of the pressure and the reference chemical potential in
both phases. This is far simpler than matching the entire distribution
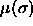 in the canonical way.
in the canonical way.
We are interested in determining the influence of polydispersity on
the hard sphere fluid-solid transition. Although the composition
distribution and hence the polydispersity cannot be imposed directly,
it can be expected that its form will be much like that of the imposed
activity-ratio distribution 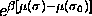 [86].
Therefore we choose the following quadratic form for the chemical
potential difference function
[86].
Therefore we choose the following quadratic form for the chemical
potential difference function

which gives rise to a Gaussian activity distribution that peaks at
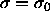 , with width
, with width  . In the limit
. In the limit 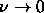 ,
the pure monodisperse
,
the pure monodisperse 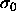 phase is recovered. For small
phase is recovered. For small  the mixture is ideal and the composition will be Gaussian with the
peak near
the mixture is ideal and the composition will be Gaussian with the
peak near 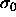 .
.
The choice of eqn.
4.3 converts Y from a functional of 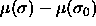 to a function of
to a function of 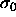 and
and  .
The fundamental thermodynamic equation now reads
.
The fundamental thermodynamic equation now reads
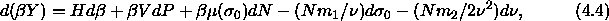
where 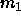 and
and 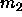 are the first and second moment of the
composition about
are the first and second moment of the
composition about 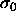 . The nth such moment is defined as
. The nth such moment is defined as

In a semigrand Monte Carlo simulation, particles sample diameters in
addition to the usual sampling of positions within the simulation box.
Diameters are sampled by selecting a particle at random, changing its
diameter by a small amount, and accepting with probability in accord
with the Metropolis algorithm. Details may be found in [87].
chapter 4
 section 4.2
section 4.2
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
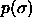 . However, this approach is
sensitive to finite size effects and, moreover, it is not practical
when phase equilibria are considered as it is difficult to ensure
chemical potential equilibration of each component. A better choice
is a grand canonical simulation in which particles of different
species are inserted and removed according to the configurational
energy and the imposed chemical potential of that component. In
this way a truly continuous distribution can be realized and phase
equilibrium can be more easily treated. However, at the high
densities of the liquid-solid equilibrium the insertion probability in
both phases is too low to obtain reasonable statistics; further, the
need to maintain the crystal structure in the solid makes insertions
especially problematic.
. However, this approach is
sensitive to finite size effects and, moreover, it is not practical
when phase equilibria are considered as it is difficult to ensure
chemical potential equilibration of each component. A better choice
is a grand canonical simulation in which particles of different
species are inserted and removed according to the configurational
energy and the imposed chemical potential of that component. In
this way a truly continuous distribution can be realized and phase
equilibrium can be more easily treated. However, at the high
densities of the liquid-solid equilibrium the insertion probability in
both phases is too low to obtain reasonable statistics; further, the
need to maintain the crystal structure in the solid makes insertions
especially problematic.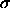 distributed according to
distributed according to 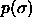 . The isobaric semigrand
canonical free energy Y is defined by a Legendre transform of the
Gibbs free energy G. In the polydisperse limit,
. The isobaric semigrand
canonical free energy Y is defined by a Legendre transform of the
Gibbs free energy G. In the polydisperse limit,
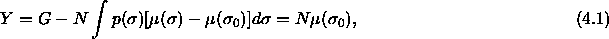

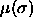 is the chemical potential as a function of
is the chemical potential as a function of
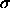 , and
, and 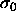 is the diameter of an arbitrarily chosen
reference component. Also, H is the enthalpy,
is the diameter of an arbitrarily chosen
reference component. Also, H is the enthalpy, 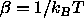 is the
reciprocal temperature, P is the pressure and V the volume of the
system. The isobaric semigrand canonical potential Y is a function of the
independent variables T,P and N and it is a functional of the
chemical potential difference function
is the
reciprocal temperature, P is the pressure and V the volume of the
system. The isobaric semigrand canonical potential Y is a function of the
independent variables T,P and N and it is a functional of the
chemical potential difference function 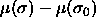 . In a simulation these independent variables must be
fixed while the thermodynamic conjugates
. In a simulation these independent variables must be
fixed while the thermodynamic conjugates 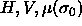 and
and 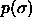 are allowed to fluctuate. This implies that the
composition
are allowed to fluctuate. This implies that the
composition 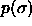 can be known only after the simulation has
been performed. Because the total number of particles is fixed the
chemical potential of the reference
can be known only after the simulation has
been performed. Because the total number of particles is fixed the
chemical potential of the reference 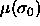 has still to be
computed. Once it is determined, the entire chemical potential
distribution is known. The method is therefore well suited for phase
equilibrium in continuous mixtures: for a given temperature and
distribution in chemical potential differences one needs match only
the values of the pressure and the reference chemical potential in
both phases. This is far simpler than matching the entire distribution
has still to be
computed. Once it is determined, the entire chemical potential
distribution is known. The method is therefore well suited for phase
equilibrium in continuous mixtures: for a given temperature and
distribution in chemical potential differences one needs match only
the values of the pressure and the reference chemical potential in
both phases. This is far simpler than matching the entire distribution
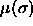 in the canonical way.
in the canonical way.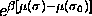 [
[
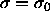 , with width
, with width  . In the limit
. In the limit 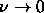 ,
the pure monodisperse
,
the pure monodisperse 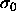 phase is recovered. For small
phase is recovered. For small  the mixture is ideal and the composition will be Gaussian with the
peak near
the mixture is ideal and the composition will be Gaussian with the
peak near 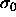 .
.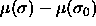 to a function of
to a function of 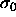 and
and  .
The fundamental thermodynamic equation now reads
.
The fundamental thermodynamic equation now reads
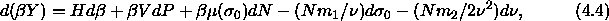
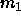 and
and 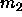 are the first and second moment of the
composition about
are the first and second moment of the
composition about 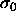 . The nth such moment is defined as
. The nth such moment is defined as
