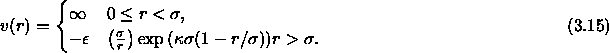
The square-well potential is often used as a crude approximation to the effective intermolecular potential in colloid-polymer mixtures. A better approximation for the colloid-colloid interaction in such systems is the hard-core attractive Yukawa potential, given by
where  is the well depth and
is the well depth and 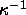 is a measure for
the range of the attractive part of the
potential [9,10,8,7]. The phase diagram of
the hard-core attractive Yukawa fluid was investigated recently by
Hagen and Frenkel [70].
To see if the solid-solid transition survives in the case of a Yukawa
potential, we did simulations on a 108 particle fcc crystal for
is a measure for
the range of the attractive part of the
potential [9,10,8,7]. The phase diagram of
the hard-core attractive Yukawa fluid was investigated recently by
Hagen and Frenkel [70].
To see if the solid-solid transition survives in the case of a Yukawa
potential, we did simulations on a 108 particle fcc crystal for
 =15, 20, 25, 30, 35, 40, 45 and 50 and in the high density
limit for
=15, 20, 25, 30, 35, 40, 45 and 50 and in the high density
limit for 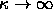 .
The densities ranged from 1.1 to 1.38. The temperatures, in reduced
units of
.
The densities ranged from 1.1 to 1.38. The temperatures, in reduced
units of 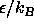 , were varied in the same range as in the
square well case, 0
, were varied in the same range as in the
square well case, 0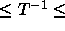 2, in steps of 0.1. For every
value of
2, in steps of 0.1. For every
value of 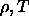 and
and  we performed some 10,000 Monte Carlo
cycles to equilibrate and the same amount to collect data. The
average internal energy was fitted to a polynomial in
we performed some 10,000 Monte Carlo
cycles to equilibrate and the same amount to collect data. The
average internal energy was fitted to a polynomial in 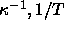 and
and 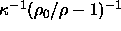 . It was not necessary
to use the more complicated functional form given in eqn.
3.4 because the energies varied much more smoothly with
density than in the square-well model.
The Helmholtz free energy of the Yukawa solid was obtained by
thermodynamic integration starting with the hard-sphere free energy
(cf. eqn.
3.2 ) and the coexistence densities as a
function of temperature were calculated by applying the double
tangent construction.
. It was not necessary
to use the more complicated functional form given in eqn.
3.4 because the energies varied much more smoothly with
density than in the square-well model.
The Helmholtz free energy of the Yukawa solid was obtained by
thermodynamic integration starting with the hard-sphere free energy
(cf. eqn.
3.2 ) and the coexistence densities as a
function of temperature were calculated by applying the double
tangent construction.
| Figure: | Simulated 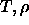 phase diagrams for the
108 particle fcc crystal structure with Yukawa potential. Starting
with the coexistence curve on the right, from right to left the
curves correspond to phase diagrams for the
108 particle fcc crystal structure with Yukawa potential. Starting
with the coexistence curve on the right, from right to left the
curves correspond to  =200, 100, 67, 50, 40, 33 and 25. The
critical points are indicated by filled circles, the triple points by
open circles. The critical point at =200, 100, 67, 50, 40, 33 and 25. The
critical points are indicated by filled circles, the triple points by
open circles. The critical point at 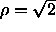 ,
corresponding to ,
corresponding to 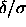 =0 was computed using the lattice
model described in section 3.2.4.
Only for the last two values the fluid-solid coexistence were
calculated. For higher =0 was computed using the lattice
model described in section 3.2.4.
Only for the last two values the fluid-solid coexistence were
calculated. For higher  values, we should expect to see the
range of stability of the solid-solid coexistence line increase
until, in the limit values, we should expect to see the
range of stability of the solid-solid coexistence line increase
until, in the limit 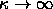 , it will extend down
to T=0. , it will extend down
to T=0. |
As in the case of the square-well model it is essential to know the
position of the fluid-solid coexistence region to determine the range
of densities where a solid-solid transition can take place.
We estimated the location of the melting curve by first-order
perturbation theory. In ref [70] it is shown that
first-order perturbation provides quite accurate estimates of the
melting curve of the hard-core attractive Yukawa system.
The Helmholtz free energy of the Yukawa system can be approximated by
where 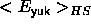 is the average value of the attractive part of
the Yukawa potential, computed in the hard-sphere reference system.
From this equation it is possible to derive the fluid-solid coexistence by
application of the double tangent construction.
Simulations on a 108 particle hard-sphere fluid and hard-sphere fcc
crystal were used to compute
is the average value of the attractive part of
the Yukawa potential, computed in the hard-sphere reference system.
From this equation it is possible to derive the fluid-solid coexistence by
application of the double tangent construction.
Simulations on a 108 particle hard-sphere fluid and hard-sphere fcc
crystal were used to compute 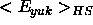 for
for 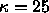 and
and
 =33.
=33.
The resulting phase diagrams for  =25, 33, 40, 50, 67, 100 and
200 are presented in figure 3.9. The solid-solid
transition is found to occur for
=25, 33, 40, 50, 67, 100 and
200 are presented in figure 3.9. The solid-solid
transition is found to occur for 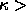 25. For values
25. For values 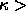 33 the fluid-solid coexistence region will shift down, which results
in a larger solid-solid two phase region. The phase diagrams of the
Yukawa solid exhibit the same overall features as those of the
square well system. The solid-solid density gap is wide at low
temperatures and shrinks when the critical point is reached. The
critical density shifts to higher values when
33 the fluid-solid coexistence region will shift down, which results
in a larger solid-solid two phase region. The phase diagrams of the
Yukawa solid exhibit the same overall features as those of the
square well system. The solid-solid density gap is wide at low
temperatures and shrinks when the critical point is reached. The
critical density shifts to higher values when  is increased,
i.e. when the range of the attractive potential is shortened.
However, in contrast to the square-well system the critical
temperature is now clearly dependent on the potential range.
The critical temperature has a value of 0.67 in the limit
is increased,
i.e. when the range of the attractive potential is shortened.
However, in contrast to the square-well system the critical
temperature is now clearly dependent on the potential range.
The critical temperature has a value of 0.67 in the limit
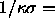 0. This was verified by direct simulations in this
limit, using the technique described in section 3.2.4. This
critical temperature is somewhat lower than for the three dimensional
square-well solid. The reason is that the Yukawa potential is
smoother than a square well. This results in an inflection point in
the free energy curve at lower temperatures. This in turn will cause
all the coexistence curves to shift to lower temperature than those
found in the square-well case.
0. This was verified by direct simulations in this
limit, using the technique described in section 3.2.4. This
critical temperature is somewhat lower than for the three dimensional
square-well solid. The reason is that the Yukawa potential is
smoother than a square well. This results in an inflection point in
the free energy curve at lower temperatures. This in turn will cause
all the coexistence curves to shift to lower temperature than those
found in the square-well case.
The value of  =25 where the solid-solid transition starts to
occur, corresponds to an average well width of
=25 where the solid-solid transition starts to
occur, corresponds to an average well width of 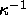 =0.04.
Although one cannot directly compare the width of a square-well and a
Yukawa potential, the characteristic well widths are of comparable magnitude.
=0.04.
Although one cannot directly compare the width of a square-well and a
Yukawa potential, the characteristic well widths are of comparable magnitude.