|
In this article, we review in detail the theory and methodology of
transition path sampling. This computational technique is an
importance sampling of reactive trajectories, the rare but important
dynamical pathways that bridge stable states. We discuss the
statistical view of dynamics underlying the method. Within this
perspective, ensembles of trajectories can be sampled and manipulated
in close analogy to standard techniques of statistical mechanics.
Because transition path sampling does not require foreknowledge of
reaction mechanisms, it is a natural tool for studying complex
dynamical structures of high-dimensional systems at the frontiers of
physics, chemistry, and biology.
The dynamics of many such systems involve rare but important
transitions between long-lived stable states. These stable states
could be, for example, distinct inherent structures of a supercooled
liquid, reactants and products of a chemical reaction, or native and
denatured states of a protein. In each case the system spends the
bulk of its time fluctuating within stable states, so that
transitions occur only rarely. In order to understand such processes
in detail, it is necessary to distinguish reaction coordinates, whose
fluctuations drive transitions between stable states, from orthogonal
variables, whose fluctuations may be viewed as random noise. In
principle, computer simulations can provide such insight. Because the
times separating successive transitions are long, however,
conventional simulations most often fail to exhibit the important
dynamics of interest.
A straightforward approach to such problems is to follow the time
evolution of the system with molecular dynamics simulations until a
reasonable number of events has been observed. The computational
requirements of such a procedure are, however, impractically
excessive for most interesting systems. For instance, a specific
water molecule in liquid water has a lifetime of about 10 hours,
before it dissociates to form hydronium and hydroxide ions. Thus,
only a few ionization events occur every hour in a system of, say,
100 water molecules. Since the simulation of molecular motions
proceeds in time steps of roughly 1 fs, approximately 10e18 steps
would be required to observe just one such event. Such a calculation
is beyond the capabilities of the fastest computers available today
and in the foreseeable future.
A different strategy, often used to study chemical reactions, is to
search for the dynamical bottlenecks the system passes through during
a transition. For a simple system, with a smooth energy landscape,
this can often
be accomplished by enumerating stationary points on the potential
energy surface. Neglecting the effects of
entropy, local minima exemplify stable (or metastable) states. Saddle
points exemplify transition states, activated states from which the
system may access different stable states via small fluctuations. One
can often infer the mechanism of a reaction by comparing stable
states and transition states. Transition rates can subsequently be
calculated by computing the reversible work to reach the transition
state from a stable state, and then initiating many fleeting
trajectories from the transition state.
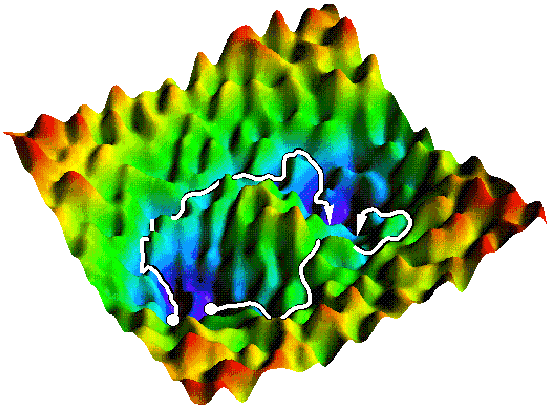
The situation is dramatically different for complex systems,
classified by Leo Kadanoff as having ``many chaotically varying
degrees of freedom interacting with one another''.
The figure in the top left corner of this page shows how one might
envision the energy landscape of such a system. As in the simple
system, long-lived stable states are separated by an energetic
barrier. But the stationary points exemplifying this barrier comprise
only a small fraction of the total set of saddle points, as is
generally the case for complex systems. An incomplete enumeration of
stationary points is thus insufficient to locate transition states of
interest. One might hope instead to guide the search for transition
states using physical intuition, in effect postulating the nature of
reaction coordinates. But these variables can be highly collective,
and therefore difficult to anticipate. In the case of electron
transfer, for instance, the relevant coordinate is an energy gap that
depends on many atomic coordinates. A specific value of the energy
gap can be realized in many different ways. Similarly, reaction
coordinates for protein folding are expected to depend on many
protein and solvent degrees of freedom.
In order to overcome these problems inherent to the study of rare
events in complex systems, we have developed a computer simulation
technique based on a statistical mechanics of
trajectories. In formulating this method, we have
recognized that transitions in complex systems may be poorly
characterized by a single sequence of configurations, such as a
minimum energy pathway. Indeed, a large set of markedly different
pathways may be relevant. We term the properly weighted set of
reactive trajectories the transition path ensemble. Defining
this ensemble does not require prior knowledge of a reaction
coordinate. Rather, it is sufficient to specify the reactants and
products of a transition. This is a crucial feature of the method,
since knowledge of a reaction coordinate is usually unavailable for
complex systems.
To sample the transition path ensemble we have developed efficient
Monte Carlo procedures that generate random walks
in the space of trajectories. As a result of this ``transition path
sampling,'' one obtains a set of reactive trajectories, from which
the reaction mechanism (or mechanisms) can be inferred. Since
trajectories generated in the transition path sampling method are
true dynamical trajectories, free of any bias, the ensemble of
harvested paths can also be used to calculate reaction rates. The
high efficiency of these algorithms has significantly widened the
range of processes amenable to computer simulation. As was
demonstrated in applications of the
methodology (see references)
the spectrum of tractable problems now includes chemical reactions in
solution, conformational transitions in biopolymers, and transport
phenomena in condensed matter systems.
In this article, we present the foundations and methodology of
transition path sampling comprehensively, including details important
for its implementation. Readers interested in a broad overview of the
perspective exploited by the method, and several of its applications,
are encouraged to consult the recent Annual Review of Physical Chemistry
article.
In the
following sections, we first discuss the theoretical basis of
transition path sampling, namely a statistical mechanics of
trajectories. We then describe how reactive trajectories may be
efficiently sampled, and subsequently analyzed. The practical
simplicity of the method is emphasized by outlining essential
algorithms in boxed summaries. Computer code exemplifying the
application of these algorithms can be downloaded from this website.
|