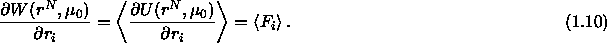chapter 1
 section 1.5
section 1.5
As we wish to use the concept of the potential of mean force later on for the
description of polymer colloid mixtures it is instructive to derive it
first for colloidal particles dispersed in a solvent. This treatment
is largely taken from Lekkerkerker et al [17].
We consider a suspension of N colloidal particles dispersed in a
solvent in a volume V which is in equilibrium with a large reservoir solely
containing the solvent. In the reservoir the solvent has a (hydrostatic) pressure 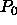 and a fugacity
and a fugacity 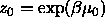 where
where
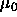 is the chemical potential of the solvent and
is the chemical potential of the solvent and 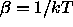 is
the inverse temperature.
Since we are imposing the fugacity of the solvent, the colloidal suspension can be
regarded an open system and the proper partition function for the
system is then
is
the inverse temperature.
Since we are imposing the fugacity of the solvent, the colloidal suspension can be
regarded an open system and the proper partition function for the
system is then
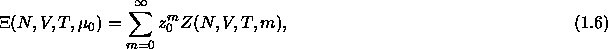
where 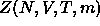 is the canonical configurational partition
function for N colloidal particles and m solvent molecules at constant
V and T
is the canonical configurational partition
function for N colloidal particles and m solvent molecules at constant
V and T
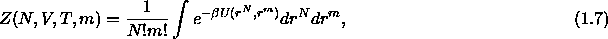
where 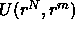 is the interaction potential of the configuration
given by the positions r of the N colloids and the m solvent molecules.
We define the potential of mean force
is the interaction potential of the configuration
given by the positions r of the N colloids and the m solvent molecules.
We define the potential of mean force 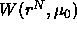 by writing the grand
canonical partition function as
by writing the grand
canonical partition function as
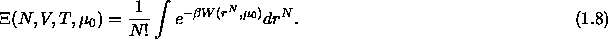
Combination of last three equation shows that the potential of mean
force is given by
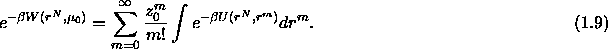
All possible solvent configurations contribute to 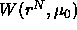 . It
is the average potential the colloidal particles feel due to all
interactions of and with the solvent. If one takes the derivative of
the
. It
is the average potential the colloidal particles feel due to all
interactions of and with the solvent. If one takes the derivative of
the 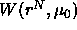 with respect to a particle's position
with respect to a particle's position 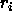 it
becomes clear why the
it
becomes clear why the 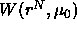 is called the potential of mean force.
is called the potential of mean force.
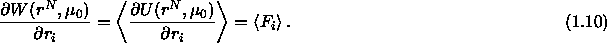
This is the average force on the colloidal particle due to the
collisions with the solvent particles.
One can connect the partition function to the thermodynamic grand potential by
the familiar equation

From this potential all the thermodynamical quantities can be
derived. For example, the osmotic pressure, which is the difference
between the pressure in the suspension and the reservoir pressure is

McMillan and Mayer also showed how the potential of mean force
approach can be used to obtain the virial expansion of the osmotic
pressure [16].
Because of the far-reaching analogy, it is possible to apply theories
that were designed for simple liquids to the phase behavior of
colloidal dispersions, and what is
more important for this thesis, it is possible to conduct
computer simulations of colloidal suspensions, as if the colloids were
large atoms interacting through the potential of mean force.
These kind of simulations can be used to test the assumptions made in
the theories,
they can provide reference data that can be compared both to
experiments and theory, and they may provide
new insights in the usually complicated phase behavior of colloidal
dispersions.
chapter 1
 section 1.5
section 1.5
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
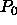 and a fugacity
and a fugacity 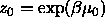 where
where
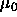 is the chemical potential of the solvent and
is the chemical potential of the solvent and 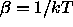 is
the inverse temperature.
Since we are imposing the fugacity of the solvent, the colloidal suspension can be
regarded an open system and the proper partition function for the
system is then
is
the inverse temperature.
Since we are imposing the fugacity of the solvent, the colloidal suspension can be
regarded an open system and the proper partition function for the
system is then
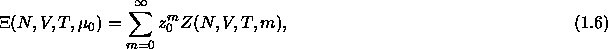
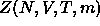 is the canonical configurational partition
function for N colloidal particles and m solvent molecules at constant
V and T
is the canonical configurational partition
function for N colloidal particles and m solvent molecules at constant
V and T
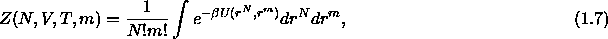
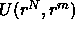 is the interaction potential of the configuration
given by the positions r of the N colloids and the m solvent molecules.
We define the potential of mean force
is the interaction potential of the configuration
given by the positions r of the N colloids and the m solvent molecules.
We define the potential of mean force 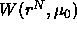 by writing the grand
canonical partition function as
by writing the grand
canonical partition function as
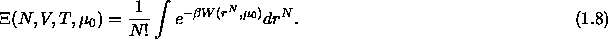
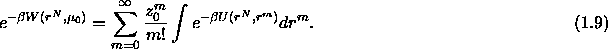
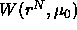 . It
is the average potential the colloidal particles feel due to all
interactions of and with the solvent. If one takes the derivative of
the
. It
is the average potential the colloidal particles feel due to all
interactions of and with the solvent. If one takes the derivative of
the 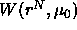 with respect to a particle's position
with respect to a particle's position 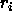 it
becomes clear why the
it
becomes clear why the 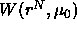 is called the potential of mean force.
is called the potential of mean force.