


Next: Simulation results Up: Binary mixtures ofhard Previous: Binary mixtures ofhard



Next: Simulation results
Up: Binary mixtures ofhard
Previous: Binary mixtures ofhard
| Figure: |
Theoretical prediction of the
phase diagram of a
system of rectangular blocks with discretized orientations [121].
The phase diagram is plotted in the 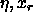 plane.
Here plane.
Here
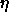 is the packing fraction and is the packing fraction and 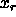 the mole fraction of rods.
The thick curves represent the phase boundaries, the thin lines are
tie-lines.
I: isotropic phase, the mole fraction of rods.
The thick curves represent the phase boundaries, the thin lines are
tie-lines.
I: isotropic phase, 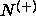 :
uniaxial rodlike nematic, :
uniaxial rodlike nematic, 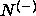 : uniaxial platelike nematic and
B: biaxial nematic. (a) : uniaxial platelike nematic and
B: biaxial nematic. (a)  =5. (b) =5. (b)  =15. =15. |
Mixtures of rod- and platelike particles may exhibit, apart from the
isotropic phase, three different types of nematic phases. A rod-rich
mixture will behave similar to a pure component rods system, and will
form a uniaxial nematic phase (denoted by 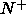 ), with the nematic
director of the rods oriented along the z-axis. The distribution of
the normals of the platelets peaks in a direction perpendicular to
the z-axis, but there is no ordering of the platelet normals in the
xy-plane.
), with the nematic
director of the rods oriented along the z-axis. The distribution of
the normals of the platelets peaks in a direction perpendicular to
the z-axis, but there is no ordering of the platelet normals in the
xy-plane.
In the opposite case of a plate-rich
mixture, the stable phase is an uniaxial discotic nematic 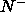 in
which the plate director lies along the z-axis and the rods
are oriented on average perpendicular to the z-axis, but without
ordering in the xy-plane. If there are approximately equal
amounts of rods and plates in the mixture, there is a possibility
that a phase will form that is absent in the pure components, namely
the biaxial
nematic phase. In this liquid
crystalline phase both species are orientationally ordered, but the
directors of the rods and platelets are
mutually perpendicular.
in
which the plate director lies along the z-axis and the rods
are oriented on average perpendicular to the z-axis, but without
ordering in the xy-plane. If there are approximately equal
amounts of rods and plates in the mixture, there is a possibility
that a phase will form that is absent in the pure components, namely
the biaxial
nematic phase. In this liquid
crystalline phase both species are orientationally ordered, but the
directors of the rods and platelets are
mutually perpendicular.
This phase behavior --- two uniaxial nematic phases separated by a biaxial one --- has been observed in several micellar systems [122,123,124,125,126,127]. These observations can indeed be explained by assuming that the micelles occur basically in two distinct shapes: rodlike and platelike shapes. But an alternative explanation of the experimental results could be that the micelles have on average a biaxial shape (i.e. with height, width and length all different). It is known, both form theory [128] and from simulation [129] that ``sufficiently'' biaxial particles can also form uniaxial and biaxial nematic phases. Which of the two models applies to the micellar systems, continues to be a matter for debate. In this chapter we present a numerical study of the phase behavior of rod-plate mixtures. In particular, we are interested in the possible stability of the biaxial nematic phase.
Before discussing these simulations, we should explain why there is still uncertainty concerning the stability of the biaxial phase. At first sight, the matter seems settled: Stroobants and Lekkerkerker [130] published a theoretical study of lyotropic (hard core) rod-plate mixtures in the Onsager approximation (neglect of virial coefficients higher than the second). They found that, for a suitable choice of the rod-rod, plate-plate and rod-plate second-virial coefficients, it was indeed possible to form a stable biaxial phase. Subsequently, Camp and Allen [131] performed numerical simulations of mixtures of prolate and oblate ellipsoids of revolution. Of course, the simulations make no assumptions about the vanishing of higher virial coefficients. In these simulations, a biaxial phase was also found. However, during the past few years, it has become increasingly clear that mixtures of convex hard particles have a much stronger tendency to phase separate than was previously assumed. In particular, Biben and Hansen [29] presented strong theoretical evidence that a binary mixture of sufficiently dissimilar hard spheres may exhibit a spinodal instability in the (possibly meta-stable) fluid phase. Similar conclusions were reached via another theoretical route by Lekkerkerker and Stroobants[132]. In addition, computer simulations provide clear evidence for demixing in a variety of hard core mixtures [133]. The mechanism that drives these demixing transitions is essentially a depletion effect: the presence of the smaller component induces an effective, entropic attraction between the larger particles. The gain in configurational entropy of smaller particles due to the clustering of the large particles outweighs the loss of configurational entropy of the large particles.
Recently, van Roij and Mulder [121] showed theoretically that
rod-plate mixtures may demix before a biaxial phase is formed, even if
the volume of the rods equals that of the plates, i.e. under
conditions where the depletion mechanism is not expected to work. The
driving force in this case is the excess average excluded volume of a
rod-plate pair as compared to that of a rod-rod or plate-plate
pair. Because this is a two-body effect (unlike the depletion
interaction, which is a three (or more) body effect), van Roij and
Mulder chose to ignore higher-order virial coefficients and
constructed an Onsager-type density functional theory. This
density-functional theory does allow for demixing. The system
considered in ref. [121] was a hard particle mixture of 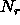 rods an
rods an 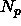 plates with restricted orientation in a volume V. The
total density is
plates with restricted orientation in a volume V. The
total density is 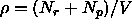 and the fraction of rods
and the fraction of rods 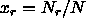 . The rods were defined by blocks of a length l and a
diameter d and the plates by blocks of width w and a height
h. The orientation of the particles was restricted to three
perpendicular directions, the x,y and z axis of the lab-frame. The
volumes of both particles were chosen to be equal,
. The rods were defined by blocks of a length l and a
diameter d and the plates by blocks of width w and a height
h. The orientation of the particles was restricted to three
perpendicular directions, the x,y and z axis of the lab-frame. The
volumes of both particles were chosen to be equal, 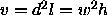 . For convenience, the aspect ratio of both particles
. For convenience, the aspect ratio of both particles 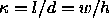 were also made equal, which leaves
were also made equal, which leaves  as the only one
free parameter. From the free energy functional van Roij and Mulder
calculated the phase diagrams for different values of
as the only one
free parameter. From the free energy functional van Roij and Mulder
calculated the phase diagrams for different values of  . In
figure 7.1 two of these diagrams are plotted in the
. In
figure 7.1 two of these diagrams are plotted in the
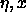 plane, where
plane, where 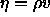 is the packing fraction of the
particles. The phase boundaries are denoted by thick curves. The thin
straight lines denote coexistence between the end points. For
is the packing fraction of the
particles. The phase boundaries are denoted by thick curves. The thin
straight lines denote coexistence between the end points. For 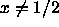 , in both cases a first order isotropic-uniaxial nematic
transition is observed which softens down to a continuous transition
at
, in both cases a first order isotropic-uniaxial nematic
transition is observed which softens down to a continuous transition
at 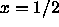 . For
. For 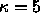 , there is a biaxial phase between the
uniaxial nematics, but it is always unstable with respect to demixing
in two coexisting
, there is a biaxial phase between the
uniaxial nematics, but it is always unstable with respect to demixing
in two coexisting 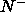 and
and 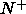 phases. In the case of
phases. In the case of  =15, they find a stable biaxial phase, which at higher packing
packing fractions again becomes unstable with respect to the demixing.
But, of course, as stressed by van Roij and Mulder, the theory in
ref. [121] is based on two important approximations: the free
energy density functional is truncated after the second virial term
and the orientations of the particles are discretized.
=15, they find a stable biaxial phase, which at higher packing
packing fractions again becomes unstable with respect to the demixing.
But, of course, as stressed by van Roij and Mulder, the theory in
ref. [121] is based on two important approximations: the free
energy density functional is truncated after the second virial term
and the orientations of the particles are discretized.
This chapter describes a simulation investigation of the possibility of
a 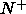 -
-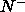 phase separation pre-empting the formation of a biaxial
phase. In order to test the theoretical predictions of van Roij
and Mulder, we initially attempted a simulation of the model used in
ref. [121], namely rectangular blocks with restricted
orientations. However, we found that this model behaves pathological
in numerical simulations. For one thing, in an MD simulation of the
restricted orientation model, it is hard to obtain equipartition of
the kinetic energy associated with motion in the x, y and z
directions. This is due to the fact that there is no momentum
transfer between the different directions, simply because all surfaces
are perpendicular or parallel to each other. Furthermore, if we try a
Gibbs-ensemble Monte Carlo (GEMC) simulation of this model system, phase separation
occurs inside the individual simulation boxes. Apparently, the
interfacial tension in a system of blocks was extremely small. As a
consequence, the Gibbs ensemble technique could not be used to study
phase separation in this model system. In view of the pathological
behavior of the restricted orientation model, we chose to simulate a
binary mixture of freely rotating ellipsoids. In the next section we
describe the simulation method and compare our results with the
theoretical phase diagrams of ref [121].
phase separation pre-empting the formation of a biaxial
phase. In order to test the theoretical predictions of van Roij
and Mulder, we initially attempted a simulation of the model used in
ref. [121], namely rectangular blocks with restricted
orientations. However, we found that this model behaves pathological
in numerical simulations. For one thing, in an MD simulation of the
restricted orientation model, it is hard to obtain equipartition of
the kinetic energy associated with motion in the x, y and z
directions. This is due to the fact that there is no momentum
transfer between the different directions, simply because all surfaces
are perpendicular or parallel to each other. Furthermore, if we try a
Gibbs-ensemble Monte Carlo (GEMC) simulation of this model system, phase separation
occurs inside the individual simulation boxes. Apparently, the
interfacial tension in a system of blocks was extremely small. As a
consequence, the Gibbs ensemble technique could not be used to study
phase separation in this model system. In view of the pathological
behavior of the restricted orientation model, we chose to simulate a
binary mixture of freely rotating ellipsoids. In the next section we
describe the simulation method and compare our results with the
theoretical phase diagrams of ref [121].
| Figure: | Computed phase diagram for a mixture of
prolate and oblate ellipsoids with an aspect ratio  =15.
In this figure, the phase diagram is shown in the P,x plane. The
pressure is expressed in units =15.
In this figure, the phase diagram is shown in the P,x plane. The
pressure is expressed in units 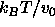 , where , where 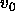 is the proper
volume of the particles. The
filled squares
denote the Gibbs ensemble results for expansion, the open squares
denote the compression results. The dotted curve is a rough estimate
for the (continuous) nematic biaxial transition. The location of the
I-N transition was obtained by matching the theoretical values of
ref. [121] to the simulation result for x=0.4. The two-phase
region a spindle shape, characteristic of mixtures that are close to ideal. is the proper
volume of the particles. The
filled squares
denote the Gibbs ensemble results for expansion, the open squares
denote the compression results. The dotted curve is a rough estimate
for the (continuous) nematic biaxial transition. The location of the
I-N transition was obtained by matching the theoretical values of
ref. [121] to the simulation result for x=0.4. The two-phase
region a spindle shape, characteristic of mixtures that are close to ideal. |


