CONCLUSION

To study the phase diagram of rodlike particles mixed with non-adsorbing polymer, we have performed simulations in a number of limiting cases, and compared the results with perturbation theory.

First of all, we simulated a system of spherocylinders with aspect ratio 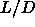=5. The effect of the added polymer was represented by an effective pair-potential. The range of this generalized square-well potential (q) is a measure for the size (radius of gyration) of the polymer. For large polymer sizes, an isotropic-isotropic phase separation takes place that ends in a critical point. This critical point shifts to higher density and higher polymer fugacity as the polymer radius is reduced. Eventually (for q<0.6), the I-I transition is preempted by the I-N transition. The perturbation theory results and our simulations on spherocylinders with a generalized square-well interaction indicate that, for 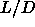=5 there is no phase separation in the nematic or smectic phase. We expect that, for very small q (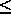0.05), there is a solid-solid transition at high densities, but we have not verified this. For large q, the I-N-SmA triple point occurs at a lower fugacity than the I-Sma-S point, but for q<0.45, the I-SmA-S triple point disappears and we are left with a I-N-SmA and a N-SmA-S triple point. The latter is located at the lower fugacity.

A nematic-nematic phase separation is possible for large 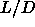. In the limit 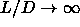, the N-N transition is not yet possible for q=1. We estimate that N-N coexistence becomes possible for q-values larger than one. For finite 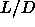-values, the q-window of stability is also bounded from the upper side, where the I-N transition will eventually preempt the N-N phase separation.

If a smectic-smectic separation occurs at all, it is likely to be confined to a narrow window in th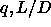e plane. At high densities and small values of q, it is possible to have isostructural solid-solid transitions, involving the plastic solid, ABC-stacked solid, and AAA-stacked solid, for small, intermediate and large 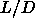-values, respectively.

We expect that polydispersity of the spherocylinders will have a pronounced effect on the phase behavior. Polydispersity in the length will stabilize the nematic phase and make a nematic-nematic transition possible at shorter (average) lengths. In contrast, polydispersity in the diameter of the spherocylinders will stabilize the smectic A phase, and could thereby favor the occurrence of a smectic-smectic phase transition.