POLYDISPERSITY

Unlike biological colloids such as viruses, proteins and blood cells, synthetic colloids are never perfectly monodisperse. The influence of this polydispersity on the phase behavior of colloidal dispersions is not well understood. In the next chapter we discuss the effect of polydispersity on the freezing of hard spheres. In this section we combine the methods of this and the next chapter to assess the influence of polydispersity on the solid-solid transition.

As will be explained in detail in the next chapter, a simulation in the semigrand ensemble is done at constant N,V,T and 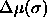. Here 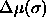is the chemical potential difference between a particle of diameter 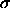, and an arbitrarily chosen reference component 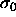and is given by

Sampling the diameters of the spheres according to this chemical potential gives rise to a Gaussian activity distribution that peaks at 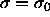, with width . For small , the size composition will also be Gaussian with the peak near 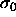and the width of this distribution is defined as the measure for size polydispersity s.

Using the same procedure as in the monodisperse case, we performed semigrand simulations for a 108 sphere system with a square well attraction in an fcc-configuration and measured the internal energy. The simulations were done for =0.02, 0.03, 0.04 and 0.05. The polydispersity ranged from 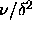=0 to 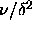=0.1. For every (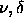) a complete set of densities was simulated for a range of temperatures. The free energy was calculated using eqn. 3.2. Coexistence was obtained by applying the common tangent construction.

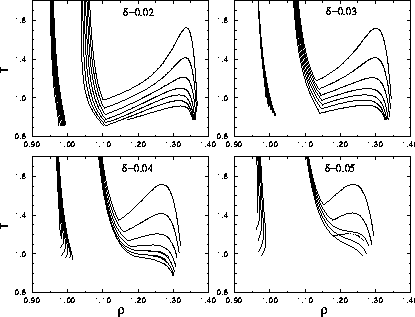
Figure 3.11 shows the dependence of the polydispersity s for different . Note that the critical temperature drops down as s increases. Table 3.3 shows the maximum value of s beyond which the solid-solid transition does not exist anymore. It appears to be essentially independent of .

chapter 3 section 3.6