section 3.5
It should be noted that isostructural solid-solid transitions are known to occur in dense Cs and Ce [71]. These transitions are believed to be due to the softness of the intermolecular potential associated with a pressure-induced change in the electronic state of the metal ions. In fact, theoretical work of Stell and Hemmer [52], and simulations of Young and Alder [55] indicate that such softness may indeed result in solid-solid transition. In the work of Kincaid, Stell and Goldmark [72] the potential is assumed to have the form of a square shoulder, a negative square well:
Using perturbation theory, Kincaid, Stell and Goldmark calculated the
isostructural solid-solid phase transition in these kind of
systems. Basically, the mechanism of this phase transition is the same
as for the square well model as described in the introduction of this chapter. At low
enough temperature, the
increase in potential energy as a function of density will be very
steep at the point when all shoulders begin to overlap. This will
induce an inflection point in the free energy curve and cause the
system to separate into two solids. There are of course
differences. Because the potential energy is now positive, instead of
negative as in the square well case, the inflection point of the free
energy, and hence the critical density, will occur at a higher
value. The other major difference will be at low temperatures, where
the system experiences effectively a hard sphere potential with a
diameter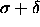 
.
We performed Monte Carlo simulations for a system of 108 particles in
a fcc crystal configuration for shoulder widths 
=0 to 
=0.08 and used eqn.
3.2 to obtain the free energy (where we had to take
negative). The solid-fluid coexistence was calculated as
well for systems with 
=0 to 
=0.08.
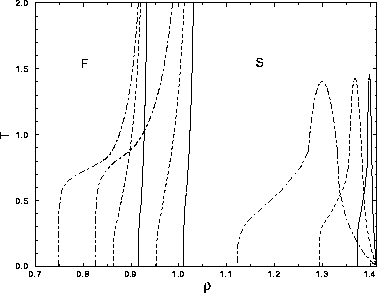
The phase diagrams for 
=0.01, 0.03 and 0.08, that were constructed as described in the
previous sections, are shown in figure 3.10. Because the
simulations did not extend beyond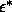 
=2, we extrapolated the
binodals to zero temperature. The differences with the attractive square well are striking:
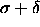and a second with a hard sphere diameter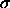 
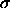hard sphere case at 
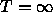to the 
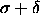hard
sphere case at T=0
Extrapolation of the critical density to larger
values of 
leads to the estimate that the solid-solid
transition will become metastable with respect to the fluid-solid
transition at roughly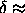 
0.25. Note that this critical
value of 
is much larger than for the square well case.
section 3.5
plane for square shoulder system. The solid curves correspond to a shoulder width 
=0.01, the dashed to 
=0.03 and the dot-dashed to 
=0.08. The fat curves indicate simulation results. The thin curves are extrapolations to the exact results at T=0.