Figure 3.1 and 3.2 show the computed solid-solid and fluid-solid coexistence curves in the 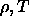plane for the two and three dimensional square-well models. We first focus on the solid-solid transition. The density gap between the dense and expanded fcc solids is wide at low temperatures and shrinks to zero when the solid-solid critical point is approached. Because of the analogy with liquid-vapor coexistence, one would expect that the solid-solid critical point should be of the 2D and 3D-Ising universality class.
The coexistence curves are asymmetric, especially in the limit 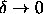. In this limit, the reduced critical temperature 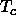goes to a finite limiting value of approximately 1.7 for D=3 and 0.92 for D=2. As we shall argue below, the phase behavior in this limit can be investigated by studying a peculiar lattice model.
As can be seen in figure 3.1 and 3.2, the critical temperature depends only weakly on . In contrast, the solid-solid coexistence region shifts to lower densities as the well-width is increased. This effect can easily be understood by noting that a dense square-well solid can be expanded at virtually no cost in potential energy, up to the point where the nearest-neighbor separation is 1+, that is 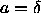. It is only when the solid is expanded beyond this limit that the potential energy increases steeply and a transition to the expanded solid may occur. Hence, the larger , the lower the density where the phase transition will take place.
The fluid-solid coexistence curves are also dependent on . For small the width of the coexistence density gap between fluid and solid remains effectively constant as a function of temperature, although as a whole it shifts to higher density as the temperature is lowered. If is increased the density gap widens at low temperature.
The point where the coexistence curves cross the solid-solid binodals is the triple point 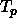where the three phases (fluid,solid I and solid II) are in equilibrium. At temperatures below the triple point the high-density solid is in equilibrium with a dilute gas. When becomes larger, the triple point shifts to higher temperatures and densities, until it reaches the critical temperature. At that point the solid-solid transition disappears because for larger values of it is preempted by the melting transition. Both in two and three dimensions, this happens when 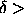0.06.
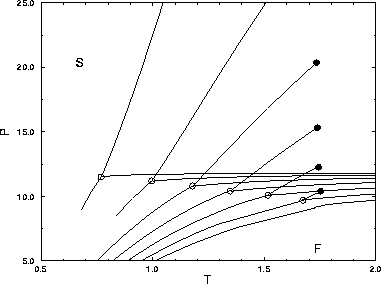
It is instructive to draw the phase diagram in the P,T plane. In figure 3.3 the phase diagrams for the three dimensional square well system are shown in the P,T plane. The solid-solid transition lines run from the triple point to the critical point and lie above the melting lines of the square well system. The phase diagram for short-ranged attractive potential is the mirror image of the usual P,T phase diagram for longer ranged potentials in which the liquid-gas transition is present. Note that the slope of the solid-solid transition line cannot be negative, because the critical temperature has to be higher than the triple point temperature.

chapter 3 section 3.2 subsection 3.2.3