chapter 3
 section 3.2
section 3.2
 subsection 3.2.2
subsection 3.2.2
Although the solid-solid transition coexistence curves can be obtained
from simulations, we have yet to demonstrate that this transition
involves phases that are thermodynamically stable.
In particular, the melting transition transition might preempt the
solid-solid phase separation. It is therefore essential to study the
fluid-solid transition as well.
We computed the solid-fluid coexistence curve by means of
thermodynamic integration. The Helmholtz free energy of square-well
solid was calculated according to eqn.
3.2 using our
simulation data. The free energy of the fluid phase was obtained by
combining data from our simulations of a square-well fluid with the
known free energy of the hard-sphere reference fluid [37].
In the two dimensional case the fluid simulations were performed on a
system consisting of 200 disks with square well potential in a
square box. The densities ranged from 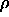 =0.81, which is below
the hard-disk fluid-solid transition at
=0.81, which is below
the hard-disk fluid-solid transition at 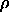 =0.87 [56],
to
=0.87 [56],
to 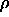 =0.95, well above the melting density.
The other simulation parameters were the same as in the two
dimensional square-well solid simulation.
=0.95, well above the melting density.
The other simulation parameters were the same as in the two
dimensional square-well solid simulation.
To simulate the fluid in three dimensions, we used a system of 108
square-well spheres in a periodic cubic box.
The density was varied from 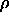 =0.9 to
=0.9 to 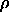 =1.0 and the well
width ranged from
=1.0 and the well
width ranged from  =0.01 to
=0.01 to  =0.06. The simulation
parameters were equal to those chosen for the solid simulations.
For both the 2D and 3D simulations the initial random configuration
was compressed to the required density and equilibrated for 20,000
cycles before data was collected in a production run of 20,000 cycles.
To calculate the fluid-solid coexistence one needs the absolute free
energy of both the reference fluid and the reference solid phase. For
the free energy of the hard disk fluid we used a Padé
approximation proposed by Hoover and Ree [56].
The hard disk solid free energy was obtained from simulation data by
Alder et al. [55].
The free energy of the hard-sphere fluid was calculated using the
accurate Carnahan-Starling equation of state [37], whereas
the Hall equation of state [54] was used in the solid region
together with an absolute free energy value obtained from simulations
of Frenkel and Ladd [39].
=0.06. The simulation
parameters were equal to those chosen for the solid simulations.
For both the 2D and 3D simulations the initial random configuration
was compressed to the required density and equilibrated for 20,000
cycles before data was collected in a production run of 20,000 cycles.
To calculate the fluid-solid coexistence one needs the absolute free
energy of both the reference fluid and the reference solid phase. For
the free energy of the hard disk fluid we used a Padé
approximation proposed by Hoover and Ree [56].
The hard disk solid free energy was obtained from simulation data by
Alder et al. [55].
The free energy of the hard-sphere fluid was calculated using the
accurate Carnahan-Starling equation of state [37], whereas
the Hall equation of state [54] was used in the solid region
together with an absolute free energy value obtained from simulations
of Frenkel and Ladd [39].
Using these reference free energies and the simulated average internal
energies in eqn.
3.2 we were able to obtain the
coexistence curves for the fluid-solid transition for both the two
and three dimensional square-well models.
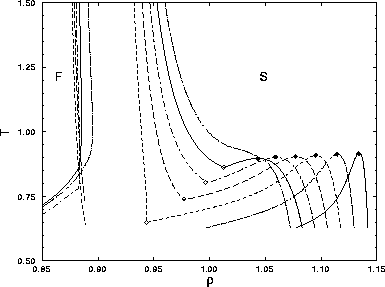
| Figure: | Simulated  phase diagrams for
triangular lattice of 200 square well particles in two dimensions.
Starting with the coexistence curve on the right, from right to left
the curves correspond to the well widths phase diagrams for
triangular lattice of 200 square well particles in two dimensions.
Starting with the coexistence curve on the right, from right to left
the curves correspond to the well widths 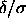 =0.01, 0.02,
0.03, 0.04, 0.05, 0.06 and 0.07. Solid-fluid coexistence curves are
shown for all systems with =0.01, 0.02,
0.03, 0.04, 0.05, 0.06 and 0.07. Solid-fluid coexistence curves are
shown for all systems with 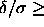 0.03. The critical
points are indicated by filled circles, the triple points by open circles. 0.03. The critical
points are indicated by filled circles, the triple points by open circles. |
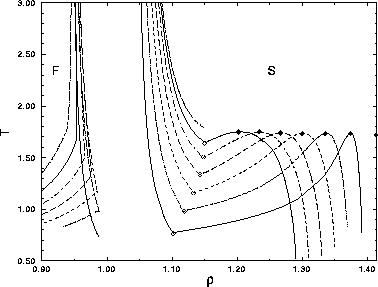
| Figure: | Simulated 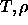 phase diagrams for the
fcc structure of 108 square well particles. Starting with the
coexistence curve on the right, from right to left the curves
correspond to the well widths phase diagrams for the
fcc structure of 108 square well particles. Starting with the
coexistence curve on the right, from right to left the curves
correspond to the well widths 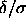 =0.01, 0.02, 0.03, 0.04,
0.05 and 0.06. The upper dashed fluid-solid coexistence curve refers
to a well width of =0.01, 0.02, 0.03, 0.04,
0.05 and 0.06. The upper dashed fluid-solid coexistence curve refers
to a well width of 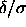 =0.07 and shows that the
solid-solid transition has become metastable at this point. The
critical points are indicated by filled circles, the triple points by
open circles. The critical point at =0.07 and shows that the
solid-solid transition has become metastable at this point. The
critical points are indicated by filled circles, the triple points by
open circles. The critical point at 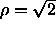 , corresponding to
, corresponding to 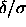 =0 was computed using the lattice
model described in section 3.2.4. =0 was computed using the lattice
model described in section 3.2.4. |
chapter 3
 section 3.2
section 3.2
 subsection 3.2.2
subsection 3.2.2
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
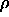 =0.81, which is below
the hard-disk fluid-solid transition at
=0.81, which is below
the hard-disk fluid-solid transition at 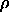 =0.87 [56],
to
=0.87 [56],
to 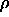 =0.95, well above the melting density.
The other simulation parameters were the same as in the two
dimensional square-well solid simulation.
=0.95, well above the melting density.
The other simulation parameters were the same as in the two
dimensional square-well solid simulation.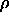 =0.9 to
=0.9 to 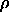 =1.0 and the well
width ranged from
=1.0 and the well
width ranged from  =0.01 to
=0.01 to  =0.06. The simulation
parameters were equal to those chosen for the solid simulations.
For both the 2D and 3D simulations the initial random configuration
was compressed to the required density and equilibrated for 20,000
cycles before data was collected in a production run of 20,000 cycles.
To calculate the fluid-solid coexistence one needs the absolute free
energy of both the reference fluid and the reference solid phase. For
the free energy of the hard disk fluid we used a Padé
approximation proposed by Hoover and Ree [56].
The hard disk solid free energy was obtained from simulation data by
Alder et al. [55].
The free energy of the hard-sphere fluid was calculated using the
accurate Carnahan-Starling equation of state [37], whereas
the Hall equation of state [54] was used in the solid region
together with an absolute free energy value obtained from simulations
of Frenkel and Ladd [39].
=0.06. The simulation
parameters were equal to those chosen for the solid simulations.
For both the 2D and 3D simulations the initial random configuration
was compressed to the required density and equilibrated for 20,000
cycles before data was collected in a production run of 20,000 cycles.
To calculate the fluid-solid coexistence one needs the absolute free
energy of both the reference fluid and the reference solid phase. For
the free energy of the hard disk fluid we used a Padé
approximation proposed by Hoover and Ree [56].
The hard disk solid free energy was obtained from simulation data by
Alder et al. [55].
The free energy of the hard-sphere fluid was calculated using the
accurate Carnahan-Starling equation of state [37], whereas
the Hall equation of state [54] was used in the solid region
together with an absolute free energy value obtained from simulations
of Frenkel and Ladd [39].
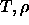 phase diagrams for
triangular lattice of 200 square well particles in two dimensions.
Starting with the coexistence curve on the right, from right to left
the curves correspond to the well widths
phase diagrams for
triangular lattice of 200 square well particles in two dimensions.
Starting with the coexistence curve on the right, from right to left
the curves correspond to the well widths 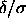 =0.01, 0.02,
0.03, 0.04, 0.05, 0.06 and 0.07. Solid-fluid coexistence curves are
shown for all systems with
=0.01, 0.02,
0.03, 0.04, 0.05, 0.06 and 0.07. Solid-fluid coexistence curves are
shown for all systems with 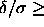 0.03. The critical
points are indicated by filled circles, the triple points by open circles.
0.03. The critical
points are indicated by filled circles, the triple points by open circles.
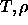 phase diagrams for the
fcc structure of 108 square well particles. Starting with the
coexistence curve on the right, from right to left the curves
correspond to the well widths
phase diagrams for the
fcc structure of 108 square well particles. Starting with the
coexistence curve on the right, from right to left the curves
correspond to the well widths 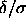 =0.01, 0.02, 0.03, 0.04,
0.05 and 0.06. The upper dashed fluid-solid coexistence curve refers
to a well width of
=0.01, 0.02, 0.03, 0.04,
0.05 and 0.06. The upper dashed fluid-solid coexistence curve refers
to a well width of 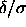 =0.07 and shows that the
solid-solid transition has become metastable at this point. The
critical points are indicated by filled circles, the triple points by
open circles. The critical point at
=0.07 and shows that the
solid-solid transition has become metastable at this point. The
critical points are indicated by filled circles, the triple points by
open circles. The critical point at 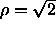 , corresponding to
, corresponding to 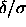 =0 was computed using the lattice
model described in section
=0 was computed using the lattice
model described in section