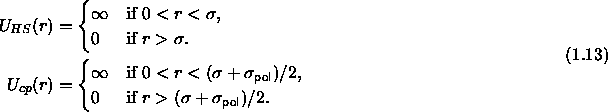chapter 1
 section 1.7
section 1.7
The range and strength of the attraction between colloids can be
varied by the addition of free non-adsorbing polymer to the colloidal
dispersion (free and non-adsorbing as opposed to the polymers used to
coat the particles for steric stabilization). These polymers, when in
an appropriate (theta-)solvent, behave as random coils with a radius
of gyration 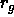 . On average, they are excluded from a shell of
thickness
. On average, they are excluded from a shell of
thickness 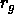 around the colloidal particle, called the depletion
zone. When two colloidal particles are brought together, these
depletion zones will overlap and the total volume accessible to the
polymer will increase. It is this increase in free volume that causes
an effective attraction; the so-called depletion force. The range of
the attraction is directly related to the radius of gyration
around the colloidal particle, called the depletion
zone. When two colloidal particles are brought together, these
depletion zones will overlap and the total volume accessible to the
polymer will increase. It is this increase in free volume that causes
an effective attraction; the so-called depletion force. The range of
the attraction is directly related to the radius of gyration 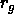 ,
whereas the strength is proportional to the osmotic pressure of the
polymers. When the diameter of the polymer is larger than
approximately 1/3 of the colloid hard-core diameter, a gas-liquid
phase separation can be observed in the phase diagram of the suspension. This
transition takes place because the increase in free energy associated
with the condenzation of the colloidal particles is more than offset
by the decrease in free energy due to the gain of free volume
accessible to the polymers. A cartoon of this phase separation is
displayed in figure 1.3.
,
whereas the strength is proportional to the osmotic pressure of the
polymers. When the diameter of the polymer is larger than
approximately 1/3 of the colloid hard-core diameter, a gas-liquid
phase separation can be observed in the phase diagram of the suspension. This
transition takes place because the increase in free energy associated
with the condenzation of the colloidal particles is more than offset
by the decrease in free energy due to the gain of free volume
accessible to the polymers. A cartoon of this phase separation is
displayed in figure 1.3.
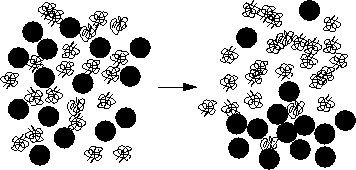
| Figure: |
Sketch of a liquid-vapor phase separation in a colloid-polymer
mixture.
The polymers gain in free volume when they push the colloidal particles
together. |
A simple, yet qualitatively correct model of polymer-colloid mixtures
was first proposed by Asakura and Oosawa [7] in the early
fifties and subsequently analyzed by Vrij [20] and Lekkerkerker
et al. [21]. In the Asakura and Oosawa (AO) model, the
colloids are represented by hard spheres of diameter 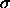 , while
the polymers are assumed to be spheres of diameter
, while
the polymers are assumed to be spheres of diameter 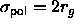 that are mutually interpenetrable, but cannot penetrate the
colloidal particles. The colloid-colloid interaction potential
that are mutually interpenetrable, but cannot penetrate the
colloidal particles. The colloid-colloid interaction potential
 and the colloid-polymer potential
and the colloid-polymer potential 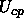 can then be written as
can then be written as
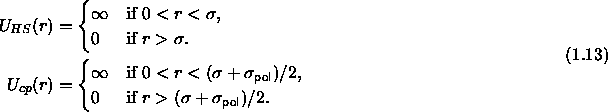
How realistic is the Asakura-Oosawa model?
The hard sphere potential is a good approximation for the
colloid-colloid interaction, certainly in the case of sterically
stabilized particles [22,8], but also for
charged colloids dissolved in a solvent with a high ionic strength
(short screening length). The assumption that the polymer are
interpenetrable is only valid for dilute solutions of polymer in a
theta-solvent [23]. The next question is, whether it is realistic to
model a polymer by a sphere. Is
the deformability of the (ideal) polymer not important? This question was the
subject of a study performed by Meijer and
Frenkel [10]. They compared
simulations of colloid-polymer mixture using the AO model, with
simulation using real, interpenetrable lattice polymers.
Meijer and Frenkel found that,
if the radius of gyration of the polymers was less that 70 % of the
radius of the colloid, the AO model works quite well .
chapter 1
 section 1.7
section 1.7
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
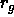 . On average, they are excluded from a shell of
thickness
. On average, they are excluded from a shell of
thickness 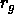 around the colloidal particle, called the depletion
zone. When two colloidal particles are brought together, these
depletion zones will overlap and the total volume accessible to the
polymer will increase. It is this increase in free volume that causes
an effective attraction; the so-called depletion force. The range of
the attraction is directly related to the radius of gyration
around the colloidal particle, called the depletion
zone. When two colloidal particles are brought together, these
depletion zones will overlap and the total volume accessible to the
polymer will increase. It is this increase in free volume that causes
an effective attraction; the so-called depletion force. The range of
the attraction is directly related to the radius of gyration 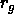 ,
whereas the strength is proportional to the osmotic pressure of the
polymers. When the diameter of the polymer is larger than
approximately 1/3 of the colloid hard-core diameter, a gas-liquid
phase separation can be observed in the phase diagram of the suspension. This
transition takes place because the increase in free energy associated
with the condenzation of the colloidal particles is more than offset
by the decrease in free energy due to the gain of free volume
accessible to the polymers. A cartoon of this phase separation is
displayed in figure 1.3.
,
whereas the strength is proportional to the osmotic pressure of the
polymers. When the diameter of the polymer is larger than
approximately 1/3 of the colloid hard-core diameter, a gas-liquid
phase separation can be observed in the phase diagram of the suspension. This
transition takes place because the increase in free energy associated
with the condenzation of the colloidal particles is more than offset
by the decrease in free energy due to the gain of free volume
accessible to the polymers. A cartoon of this phase separation is
displayed in figure 1.3.

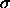 , while
the polymers are assumed to be spheres of diameter
, while
the polymers are assumed to be spheres of diameter 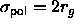 that are mutually interpenetrable, but cannot penetrate the
colloidal particles. The colloid-colloid interaction potential
that are mutually interpenetrable, but cannot penetrate the
colloidal particles. The colloid-colloid interaction potential
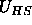 and the colloid-polymer potential
and the colloid-polymer potential 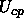 can then be written as
can then be written as