chapter 1
 section 1.3
section 1.3
Since the work of van der Waals [4], we know that there is no
essential distinction between a liquid and a vapor. Above the critical
temperature 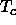 , a vapor can be compressed continuously all the way to the
freezing
point. Yet below
, a vapor can be compressed continuously all the way to the
freezing
point. Yet below 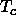 , a first-order phase transition separates the dilute
fluid (vapor) from the dense fluid (liquid).
In the van der Waals model the molecules are described by hard
spheres with an infinitely weak, infinitely long-ranged
attraction. Application of thermodynamic perturbation theory results in the complete phase
diagram for the van der Waals model. The diagram in the density-temperature phase plane shown in
figure 1.2a includes besides the usual liquid vapor transition
also crystallization. This feature was not
incorporated in the original van der Waals equation because the hard sphere
crystallization transition was not recognized at the time.
At high temperatures the molecules behave effectively as hard
spheres, which show only crystallization but do not have a liquid vapor
transition [2]. At lower temperatures, between the critical point and the
triple point temperature a liquid-vapor transition is possible.
Below the triple-point temperature the liquid phase
becomes meta-stable and there is only a gas-solid transition.
Although the van der Waals theory becomes exact in the limit of weak,
long-ranged intermolecular interactions [5], there is no
fundamental reason why the liquid-vapor transition
should occur in every atomic or molecular substance, nor is there any
rule that forbids the existence of more than one fluid-fluid
transition.
, a first-order phase transition separates the dilute
fluid (vapor) from the dense fluid (liquid).
In the van der Waals model the molecules are described by hard
spheres with an infinitely weak, infinitely long-ranged
attraction. Application of thermodynamic perturbation theory results in the complete phase
diagram for the van der Waals model. The diagram in the density-temperature phase plane shown in
figure 1.2a includes besides the usual liquid vapor transition
also crystallization. This feature was not
incorporated in the original van der Waals equation because the hard sphere
crystallization transition was not recognized at the time.
At high temperatures the molecules behave effectively as hard
spheres, which show only crystallization but do not have a liquid vapor
transition [2]. At lower temperatures, between the critical point and the
triple point temperature a liquid-vapor transition is possible.
Below the triple-point temperature the liquid phase
becomes meta-stable and there is only a gas-solid transition.
Although the van der Waals theory becomes exact in the limit of weak,
long-ranged intermolecular interactions [5], there is no
fundamental reason why the liquid-vapor transition
should occur in every atomic or molecular substance, nor is there any
rule that forbids the existence of more than one fluid-fluid
transition.
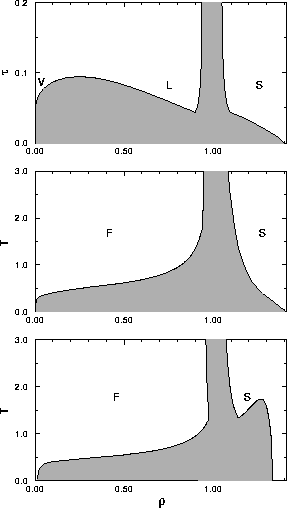
| Figure 1.2 : | Generic temperature--density phase diagrams. Top: The van der Waals
limit shows besides the fluid-solid transition a liquid-vapor transition. Middle: for a medium ranged
potential the liquid phase becomes metastable. Bottom: For very short ranged
potentials the critical point reappears inside the solid phase. Here,
a expanded solid is in coexistence with a condensed crystal. |
Whether a given compound will
have a liquid phase, depends sensitively on the range of the intermolecular
potential: as this range is decreased,
the critical temperature
approaches the triple-point temperature, and when 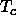 drops below
the latter, only a single stable fluid phase remains (see figure 1.2b).
This phenomenon is well
known in mixtures of spherical colloidal particles and non-adsorbing polymer,
where the range of the
attractive part of the effective colloid-colloid interaction can be varied by
changing the size of the
polymer [6,7,8,9,10].
Experiment, theory and simulation all suggest that when the
width of the attractive well becomes less than approximately one third of the
diameter of the colloidal spheres, the colloidal `liquid' phase disappears.
In fact,
there is numerical evidence that in a molecular compound (
drops below
the latter, only a single stable fluid phase remains (see figure 1.2b).
This phenomenon is well
known in mixtures of spherical colloidal particles and non-adsorbing polymer,
where the range of the
attractive part of the effective colloid-colloid interaction can be varied by
changing the size of the
polymer [6,7,8,9,10].
Experiment, theory and simulation all suggest that when the
width of the attractive well becomes less than approximately one third of the
diameter of the colloidal spheres, the colloidal `liquid' phase disappears.
In fact,
there is numerical evidence that in a molecular compound (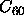 ), the
range of the intermolecular attraction may be sufficiently short to suppress
the liquid-vapor transition [11,12].
The fact that the liquid-vapor transition is just metastable can
result in special properties. For example, most successful
crystallizations of globular proteins have been carried out under
circumstances where the liquid-vapor transition was
suppressed [13]. Apparently, the absence of an
intermediate
liquid phase is of great importance for the
success of protein crystallization.
), the
range of the intermolecular attraction may be sufficiently short to suppress
the liquid-vapor transition [11,12].
The fact that the liquid-vapor transition is just metastable can
result in special properties. For example, most successful
crystallizations of globular proteins have been carried out under
circumstances where the liquid-vapor transition was
suppressed [13]. Apparently, the absence of an
intermediate
liquid phase is of great importance for the
success of protein crystallization.
As will be discussed later in this thesis,
systems with a very short-ranged interaction may exhibit a novel type
of phase
transition that occurs entirely at the solid phase side
of the phase diagram, but is otherwise in many ways reminiscent of the
liquid-vapor transition (see figure 1.2c).
Again this kind of phase behavior should be observable in certain
colloid-polymer
mixtures (although, at the time this thesis is written, it has not yet
been observed).
Because the properties of colloidal dispersions and colloid-polymer mixtures constitute
the main themes of this
thesis, we first explain what they are.
chapter 1
 section 1.3
section 1.3
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
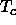 , a vapor can be compressed continuously all the way to the
freezing
point. Yet below
, a vapor can be compressed continuously all the way to the
freezing
point. Yet below 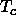 , a first-order phase transition separates the dilute
fluid (vapor) from the dense fluid (liquid).
In the van der Waals model the molecules are described by hard
spheres with an infinitely weak, infinitely long-ranged
attraction. Application of thermodynamic perturbation theory results in the complete phase
diagram for the van der Waals model. The diagram in the density-temperature phase plane shown in
figure 1.2a includes besides the usual liquid vapor transition
also crystallization. This feature was not
incorporated in the original van der Waals equation because the hard sphere
crystallization transition was not recognized at the time.
At high temperatures the molecules behave effectively as hard
spheres, which show only crystallization but do not have a liquid vapor
transition [2]. At lower temperatures, between the critical point and the
triple point temperature a liquid-vapor transition is possible.
Below the triple-point temperature the liquid phase
becomes meta-stable and there is only a gas-solid transition.
Although the van der Waals theory becomes exact in the limit of weak,
long-ranged intermolecular interactions [5], there is no
fundamental reason why the liquid-vapor transition
should occur in every atomic or molecular substance, nor is there any
rule that forbids the existence of more than one fluid-fluid
transition.
, a first-order phase transition separates the dilute
fluid (vapor) from the dense fluid (liquid).
In the van der Waals model the molecules are described by hard
spheres with an infinitely weak, infinitely long-ranged
attraction. Application of thermodynamic perturbation theory results in the complete phase
diagram for the van der Waals model. The diagram in the density-temperature phase plane shown in
figure 1.2a includes besides the usual liquid vapor transition
also crystallization. This feature was not
incorporated in the original van der Waals equation because the hard sphere
crystallization transition was not recognized at the time.
At high temperatures the molecules behave effectively as hard
spheres, which show only crystallization but do not have a liquid vapor
transition [2]. At lower temperatures, between the critical point and the
triple point temperature a liquid-vapor transition is possible.
Below the triple-point temperature the liquid phase
becomes meta-stable and there is only a gas-solid transition.
Although the van der Waals theory becomes exact in the limit of weak,
long-ranged intermolecular interactions [5], there is no
fundamental reason why the liquid-vapor transition
should occur in every atomic or molecular substance, nor is there any
rule that forbids the existence of more than one fluid-fluid
transition.

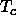 drops below
the latter, only a single stable fluid phase remains (see figure
drops below
the latter, only a single stable fluid phase remains (see figure 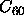 ), the
range of the intermolecular attraction may be sufficiently short to suppress
the liquid-vapor transition [
), the
range of the intermolecular attraction may be sufficiently short to suppress
the liquid-vapor transition [