The early Greek natural philosophers already knew that all matter could be classified in one of the four primary elements: air, water, earth and fire. Nowadays, this classification is still largely valid, although we now use the word ``phases'' where the Greek spoke about ``elements''. The four most abundant phases of matter are the vapor, the liquid, the solid and the plasma. (The last phase is a special case because it does not consist of the same building blocks as the other three: it is basically an ionized gas).
Matter can transform from one phase to the other by a ``phase transition''. For instance, increasing the temperature of a liquid results in boiling and evaporation. Different phases can be in equilibrium with each other, coexisting together, without changing visibly in time. An example is the hot coffee in our thermos flask, where the liquid coffee is in equilibrium with its vapor. Atoms move continuously from the liquid to the vapor phase and vice versa, but on average the situation does not change.
How can we establish the properties of such coexisting phases? This question can be answered by thermodynamics [1]. In equilibrium a system has minimized its free energy. This minimized free energy F will in general be a complicated function of the volume V and the number of particles N (both extensive parameters), and the temperature T (an intensive parameter). The precise form of the dependence of F on N, V and T is determined by the

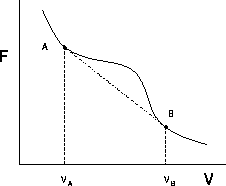
| Figure 1.1: | Free energy curve with an instable
region between 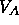 and and 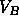 |
Hamiltonian of the system.
In figure 1.1 we show a schematic plot of the free energy
F as a function of the volume V. At small V , i.e. high density, we
have, for instance, a liquid phase. Expanding the volume at constant
temperature,
the free energy of the system will follow the curve, until point A
is reached. Beyond that point the system can lower its total free
energy by splitting up into two phases, one with 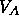 and one with
and one with
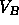 . As it is extensive, the free energy of the total system is just a linear combination of the free
energy of the liquid and that of the vapor phase, as indicated by
the dotted straight
line.
If we increase the volume, more and more liquid will evaporate, but
the densities of the coexisting phases remain fixed. When the volume
reaches point B, there is only a vapor phase and the free energy follows
the solid line again.
The coexisting densities are determined by the coexistence relations
. As it is extensive, the free energy of the total system is just a linear combination of the free
energy of the liquid and that of the vapor phase, as indicated by
the dotted straight
line.
If we increase the volume, more and more liquid will evaporate, but
the densities of the coexisting phases remain fixed. When the volume
reaches point B, there is only a vapor phase and the free energy follows
the solid line again.
The coexisting densities are determined by the coexistence relations
where 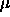 denotes the chemical potential. These densities can be found directly from the free energy curve by the so-called
``common tangent construction'' [1]. The tangents of the free energy curve
at points A and B have to be equal to the slope of the straight line
connecting those points. This geometrical procedure is equivalent to imposing
eqn.
1.5. The kind of phase transition we discussed above is called
first-order and can be recognized by the difference in density
between two coexisting phases. In contrast, during a continuous (or
second-order) phase transition, the system will lower its free energy
by undergoing a
transformation from one phase
to the other at a single density, instead of splitting up
in two distinct coexisting phases.
denotes the chemical potential. These densities can be found directly from the free energy curve by the so-called
``common tangent construction'' [1]. The tangents of the free energy curve
at points A and B have to be equal to the slope of the straight line
connecting those points. This geometrical procedure is equivalent to imposing
eqn.
1.5. The kind of phase transition we discussed above is called
first-order and can be recognized by the difference in density
between two coexisting phases. In contrast, during a continuous (or
second-order) phase transition, the system will lower its free energy
by undergoing a
transformation from one phase
to the other at a single density, instead of splitting up
in two distinct coexisting phases.
The properties of coexisting phases can be plotted as
a function of thermodynamic control variables in a phase diagram. The
common P-T
diagram consists of curves delimiting the areas in pressure-temperature space where
a single phase is stable.
Phase transitions can be indicated in a P-T diagram by single
curves because, at coexistence, both the pressure and the temperature of
the two phases are equal. In contrast, if we were to indicate the
location of a phase transition in a temperature-density 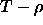 diagram, the curves that describe the densities of the coexisting
phases do not coincide, because there is no thermodynamic condition
stating that the densities of coexisting phases should be equal.
Hence, in a
diagram, the curves that describe the densities of the coexisting
phases do not coincide, because there is no thermodynamic condition
stating that the densities of coexisting phases should be equal.
Hence, in a 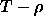 diagram, stable
phase regions are separated by a density gap, called the two phase
or coexistence region, where neither pure phase is stable and the
system is forced to phase separate.
diagram, stable
phase regions are separated by a density gap, called the two phase
or coexistence region, where neither pure phase is stable and the
system is forced to phase separate.