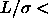 0.3 and a liquid phase will not be stable for these rod lengths.
We expect that for very short rods the critical point will reappear in
the solid phase. In the next chapter we show that in systems with very
short ranged attraction a phase transition can occur between a dense
packed crystal and a less dense crystal (see also ref. [41]). This phase transition is first order, ends in a critical point and is similar to the liquid-vapor transition.
0.3 and a liquid phase will not be stable for these rod lengths.
We expect that for very short rods the critical point will reappear in
the solid phase. In the next chapter we show that in systems with very
short ranged attraction a phase transition can occur between a dense
packed crystal and a less dense crystal (see also ref. [41]). This phase transition is first order, ends in a critical point and is similar to the liquid-vapor transition.The features of the phase diagrams of the rodlike polymer are completely comparable with that of the fully flexible chains [10], although in the latter case the disappearing of the liquid region is predicted at polymer radii of gyration 2
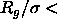 0.45.
However, the latter estimate is quite crude. It is therefore not obvious that the difference with the value obtained here is significant.
0.45.
However, the latter estimate is quite crude. It is therefore not obvious that the difference with the value obtained here is significant.The liquid-gas separation in the rod like polymer colloid mixture can be described by first order perturbation theory. This theory predicts the location of the critical point well at rod lengths
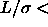 4,
although this accuracy decreases for higher values of
4,
although this accuracy decreases for higher values of 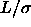 . The
perturbation theory is accurate because the rods do not significantly
affect the structure of the hard sphere dispersion. Hence, the free volume for a rod in a dispersion of spheres is effectively independent of the concentration of rods. Of course this is only valid in the case of ideal polymers. If the polymers would interact with each other the free volume would decrease considerably with the fugacity.
. The
perturbation theory is accurate because the rods do not significantly
affect the structure of the hard sphere dispersion. Hence, the free volume for a rod in a dispersion of spheres is effectively independent of the concentration of rods. Of course this is only valid in the case of ideal polymers. If the polymers would interact with each other the free volume would decrease considerably with the fugacity.In the limit
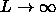 , the critical point shifts to zero density and zero polymer fugacity. The binodal curve is in this limit equivalent to the equation of state for hard spheres. The fugacity of the rods is equal to the pressure of the coexisting hard sphere fluid phase because in the vapor phase no spheres are present and the liquid phase is free of needles.
This fact may provide an alternative route to obtain the equation of state of hard spheres experimentally by measuring the concentration of rods in the vapor phase of a phase separated mixture of colloids and stiff polymers as a function of the volume fraction of spheres in the liquid phase.
, the critical point shifts to zero density and zero polymer fugacity. The binodal curve is in this limit equivalent to the equation of state for hard spheres. The fugacity of the rods is equal to the pressure of the coexisting hard sphere fluid phase because in the vapor phase no spheres are present and the liquid phase is free of needles.
This fact may provide an alternative route to obtain the equation of state of hard spheres experimentally by measuring the concentration of rods in the vapor phase of a phase separated mixture of colloids and stiff polymers as a function of the volume fraction of spheres in the liquid phase.The simulations discussed in this chapter show that for mixtures of hard spherical particles and thin needles liquid-vapor phase separation will occur. However, one could object that the limiting case of infinitely thin needles is unrealistic. Hence, it is important to know whether the demixing transition will still occur if the needles have a finite diameter D. Recently, Mao et al. [42] have investigated the effect of the finite thickness of the rods on the potential of mean force between two spheres. They find that, for rods of finite thickness, the effective pair potential develops a repulsive barrier at finite separation, in addition to the attractive well at contact. In particular for small
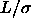 values, this barrier can be high enough to lead
to kinetic stabilization of the suspension and prevent any phase separation.
values, this barrier can be high enough to lead
to kinetic stabilization of the suspension and prevent any phase separation.
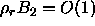 ,
where
,
where 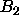 is the second virial coefficient of the rods and
is the second virial coefficient of the rods and 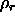 their number density. To see at what value of the rod osmotic pressure the isotropic-nematic transition occurs, we consider
the Onsager limit of rods with high
their number density. To see at what value of the rod osmotic pressure the isotropic-nematic transition occurs, we consider
the Onsager limit of rods with high 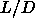 ratio [
ratio [
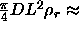 3.3 [
3.3 [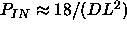 .
To observe the liquid-vapor phase separation, this pressure has to be larger than the critical pressure
.
To observe the liquid-vapor phase separation, this pressure has to be larger than the critical pressure 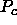 for the phase separation.
for the phase separation.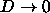 while L remains finite, the I-N transition occurs at infinite pressure.
For rods with a finite diameter, demixing can compete with the I-N transition. To
be specific, on basis of the perturbation theory and
eqn.
while L remains finite, the I-N transition occurs at infinite pressure.
For rods with a finite diameter, demixing can compete with the I-N transition. To
be specific, on basis of the perturbation theory and
eqn.
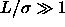 ,
, 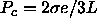 . If we equate
. If we equate 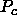 to
to 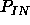 , we find that
demixing is preempted by an I-N transition if
, we find that
demixing is preempted by an I-N transition if 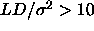 .
This implies that for small
.
This implies that for small 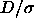 the liquid-vapor phase
separation occurs well before the I-N transition.
the liquid-vapor phase
separation occurs well before the I-N transition.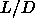 ratios. This will probably
shift the phase separation region as well as the isotropic-nematic
transition to higher fugacities. So we expect that the liquid-vapor
phase separation still occurs at lower fugacities than the
isotropic-nematic transition for reasonable
ratios. This will probably
shift the phase separation region as well as the isotropic-nematic
transition to higher fugacities. So we expect that the liquid-vapor
phase separation still occurs at lower fugacities than the
isotropic-nematic transition for reasonable 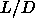 ratios (
ratios (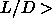 5),
provided that the transition is not prevented by any kinetic
stabilization [
5),
provided that the transition is not prevented by any kinetic
stabilization [