chapter 2 section 2.3 subsection 2.3.2

THE LIMIT

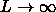
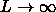
The liquid-vapor coexistence terminates in a critical point. If the rod length increases the critical density shifts to lower values. For 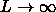this density is proportional to 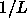, as can be derived from perturbation theory by setting the first and second derivative of the pressure (eqn. 2.14) with respect to the density equal to zero. The critical volume fraction 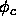then follows as a function of L

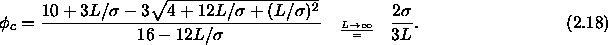
Using this result we can obtain the critical rod fugacity from eqn. 2.14 as well.

Another remarkable fact is that the theoretical coexistence curve has a simple asymptotic form for very long rod lengths. If the critical density becomes zero the hard sphere vapor density also has to vanish. In this region the liquid vapor coexistence curve is easy to calculate by equating the pressures of the liquid and the vapor phase. The chemical potential is not important in the limit of long rods because the coexistence density of the vapor is effectively independent of the chemical potential. In the vapor phase the pressure is simply equal to the fugacity of the rods because there are no spheres present. The pressure in the fluid phase follows from eqn. 2.14

In the 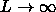limit the free volume fraction 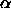available to the rods in the liquid vanishes. The pressure of the fluid therefore reduces to the hard sphere equation of state. Equating the pressure in both phases gives

This result provides an alternative route to measure the hard sphere equation of state in experiments by measuring the rod concentration of the vapor phase as a function of the density of spheres in the liquid phase.

chapter 2 section 2.3 subsection 2.3.2